
【题目】解下列方程:
(1)解方程::x2﹣6x﹣5=0; (2)解方程:2(x﹣1)2=3x﹣3;
(3)求抛物线![]() 的顶点坐标、对称轴和它与坐标轴的交点坐标.
的顶点坐标、对称轴和它与坐标轴的交点坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)运用配方法求解即可;
(2)移项后提取公因式(x-1),即可得出两个一元一次方程,求出方程的解即可;
(3)提取-1,再配方,即可得出y=-(x-2)2+1,得出答案即可.
(1)移项得x2﹣6x=5,
方程两边都加上9得 x2﹣6x+9=5+9,
即 (x﹣3)2=14,
则x﹣3=±![]() ,
,
所以x1=3+![]() ,x2=3﹣
,x2=3﹣![]() ;
;
(2)原方程变形为:2(x﹣1)2=3(1﹣x),
即:(x﹣1)(2x+1)=0,
即x﹣1=0,2x+1=0,
解得x1=1,x2=﹣![]() ;
;
(3)![]()
=-(x-2)2+1
∴顶点坐标是(2,1),对称轴是直线![]() .
.
令y=0,得,-(x-2)2+1=0,
解得,![]()
∴与x轴交点(1,0)(3,0),
令x=0,则y=-3,
∴与y轴交点(0,-3)


科目:初中数学 来源: 题型:
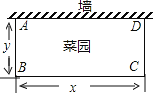
【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A. y=-2x+24(0<x<12) B. y=-![]() x+12(0<x<24)
x+12(0<x<24)
C. y=2x-24(0<x<12) D. y=![]() x-12(0<x<24)
x-12(0<x<24)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品现在的售价为每件60元,每星期可卖出300件. 市场调查反映:如调整价格,每降价1元,每星期可多卖出20件. 已知商品的进价为每件40元,如何定价才能使利润最大?这个最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图一次函数y1=-x-2与y2=x-4的图象相交于点A.
(1)求点A的坐标;
(2)若一次函数y1=-x-2与y2=x-4的图象与x轴分别相交于点B、C,求△ABC的面积.
(3)结合图象,直接写出y1>y2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
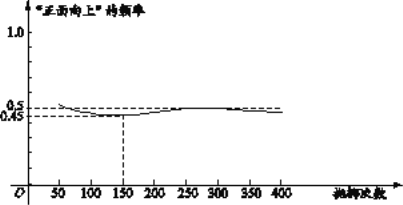
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
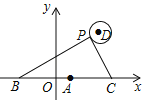
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
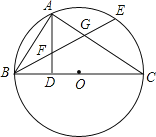
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com