
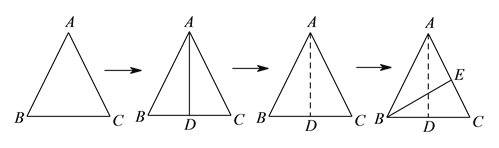
【题目】如图,将边长为![]() 的正三角形纸片
的正三角形纸片![]() 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕![]() ,
, ![]() (如图①),点
(如图①),点![]() 为其交点.
为其交点.
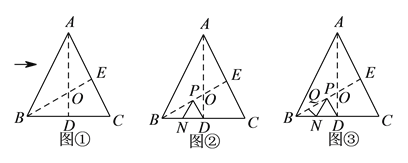
(![]() )探求
)探求![]() 到
到![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )如图②,若
)如图②,若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 上的动点.
上的动点.
①当![]() 的长度取得最小值时,求
的长度取得最小值时,求![]() 的长度.
的长度.
②如图③,若点![]() 在线段
在线段![]() 上,
上, ![]() ,则
,则![]() 的最小值
的最小值![]() __________.
__________.
【答案】(![]() )
)![]() ;(
;(![]() )①
)①![]() ;②
;②![]() 最小值为
最小值为![]() .
.
【解析】试题分析:(1)根据等边三角形的性质得到∠BAO=∠ABO=∠OBD=30°,得到AO=OB,根据直角三角形的性质即可得到结论;
(2)如图②,作点D关于BE的对称点D′,过D′作D′N⊥BC于N交BE于P,则此时PN+PD的长度取得最小值,根据线段垂直平分线的想知道的BD=BD′,推出△BDD′是等边三角形,得到BN的长,于是得到结论;
(3)如图③,作Q关于BC的对称点Q′,作D关于BE的对称点D′,连接Q′D′,即为QN+NP+PD的最小值.根据轴对称的定义得到∠Q′BN=∠QBN=30°,∠QBQ′=60°,得到△BQQ′为等边三角形,△BDD′为等边三角形,解直角三角形即可得到结论.
试题解析:解:(1)AO=2OD.理由:∵△ABC是等边三角形,∴∠BAO=∠ABO=∠OBD=30°,∴AO=OB.∵BD=CD,∴AD⊥BC,∴∠BDO=90°,∴OB=2OD,∴OA=2OD;
(2)如图②,作点D关于BE的对称点D′,过D′作D′N⊥BC于N交BE于P,则此时PN+PD的长度取得最小值.∵BE垂直平分DD′,∴BD=BD′.∵∠ABC=60°,∴△BDD′是等边三角形,∴BN=![]() BD=
BD=![]() .∵∠PBN=30°,∴
.∵∠PBN=30°,∴![]() ,∴PB=
,∴PB=![]() ;
;
(3)如图③,作Q关于BC的对称点Q′,作D关于BE的对称点D′,连接Q′D′,即为QN+NP+PD的最小值.
根据轴对称的定义可知:∠Q′BN=∠QBN=30°,∠QBQ′=60°,∴△BQQ′为等边三角形,△BDD′为等边三角形,∴∠D′BQ′=90°.在Rt△D′BQ′中,D′Q′=![]() =
=![]() ,∴QN+NP+PD的最小值=
,∴QN+NP+PD的最小值=![]() ,故答案为:
,故答案为: ![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,

求:(1)在图(1)中∠B+∠D=?(2)在图(2)中∠B+∠E1+∠D=?(3)在图(3)中∠B+∠E1+∠E2+…+∠En﹣1+∠En+∠D=?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)在(1)的图形中,找出两条相等的线段,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(1+a)(1-a)+(a-2)2,其中a=![]() ;
;
(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2,其中x=-3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的文字,然后解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() ﹣1表示
﹣1表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:如果![]() =x+y,其中x是整数,且0<y<1,那么x=1,y=
=x+y,其中x是整数,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
请解答下列问题:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= ,b= ;
=a+b,其中a是整数,且0<b<1,那么a= ,b= ;
(2)已知2+![]() =m+n,其中m是整数,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整数,且0<n<1,求|m﹣n|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高致病性禽流感是比SARS传染速度更快的传染病.为防止禽流感蔓延,政府规定:离疫点3km范围内为扑杀区;离疫点3km~5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
(1)请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);
(2)求这条公路在免疫区内有多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com