
分析 (1)根据方程的系数结合根的判别式即可得出△=(m-3)2≥0,由此即可证出结论;
(2)由等腰三角形的性质可知b=c或b、c中有一个为6,①当b=c时,根据根的判别式△=(m-3)2=0,解之求出m值,将m的值代入原方程中解方程即可得出方程的解,再根据三角形的三边关系即可得出该种情况不合适;②当方程的一根为6时,将x=6代入原方程求出m值,将m的值代入原方程中解方程即可得出方程的解,再根据三角形的三边关系确定△ABC的三条边,结合三角形的周长即可得出结论.
解答 解:(1)证明:∵在方程x2-(m+1)x+2(m-1)=0中,△=[-(m+1)]2-4×2(m-1)=m2-6m+9=(m-3)2≥0,
∴无论m取何值,这个方程总有实数根;
(2)∵△ABC为等腰三角形,
∴b=c或b、c中有一个为6.
①当b=c时,△=(m-3)2=0,
解得:m=3,
∴原方程为x2-4x+4=0,
解得:b=c=2,
∵b+c=2+2=4<6,
∴2、2、6不能构成三角形.
②当方程的一根为6时,将x=6代入原方程得:36-6(m+1)+2(m-1)=0,
解得:m=7,
∴原方程为x2-8x+12=0,
解得:x1=2,x2=6,
∵6+2=8>6,6+6=12>2,
∴△ABC的三边长为:2、6、6,
∴C△ABC=2+6+6=14.
点评 本题考查了根的判别式、三角形三边关系以及等腰三角形的性质,根据等腰三角形的性质分b=c或b、c中有一个为6两种情况考虑是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
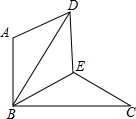 如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°而得,且AB⊥BC,BE=CE,连接DE.
如图,△BAD是由△BEC在平面内绕点B逆时针旋转60°而得,且AB⊥BC,BE=CE,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-2 | B. | x<5 | C. | x<2 | D. | -2<x<5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com