
【题目】如图,P是矩形ABCD内一点,连结P与矩形ABCD各顶点,矩形EFGH各顶点分别在边AP,BP,CP,DP上,已知AE=2EP,EF∥AB,图中两块阴影部分的面积和为S.则矩形ABCD的面积为( )
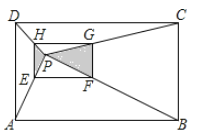
A.4SB.6SC.12SD.18S
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
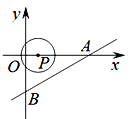
【题目】如图,直线![]() 交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是______________.
交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 经过点
经过点![]() ,且满足9a+3b+c<0,以下结论:①a+b<0;②4a+c<0;③对于任何x,都有
,且满足9a+3b+c<0,以下结论:①a+b<0;②4a+c<0;③对于任何x,都有![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
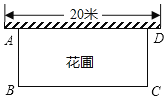
【题目】阿静家在新建的楼房旁围成一个矩形花圃,花圃的一边利用20米长的院墙,另三边用总长为32米的离笆恰好围成.如图,设AB边的长为x米,矩形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围.
(2)当x为何值时,S有最大值?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张准备给长方形客厅铺设瓷砖,已知客厅长AB=8m,宽BC=6m,现将其划分成一个长方形EFGH区域I和环形区域Ⅱ,区域Ⅰ用甲、乙瓷砖铺设,其中甲瓷砖铺设成的是两个全等的菱形图案,区域Ⅱ用丙瓷砖铺设,如图所示,已知N是GH中点,点M在边HE上,HN=3HM,设HM=x(m).
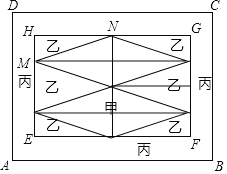
(1)用含x的代数式表示以下数量.铺设甲瓷砖的面积为 m2,铺设丙瓷砖的面积为 m2.
(2)若甲、乙、丙瓷砖单价分别为300元/m2,200元/m2,100元/m2,且EF≥FG+2,铺设好整个客厅,三种瓷砖总价至少需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() (如图),点
(如图),点![]() ,
,![]() 分别为射线
分别为射线![]() 上的动点(点C、E都不与点B重合),连接AC、AE使得
上的动点(点C、E都不与点B重合),连接AC、AE使得![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
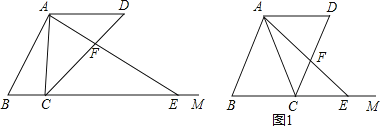
(1)如图1,当![]() 时,求AF的长.
时,求AF的长.
(2)当点![]() 在点
在点![]() 的右侧时,求
的右侧时,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.
(3)连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,直接写出
是等腰三角形,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,在RT△ABC中,∠C=90°,BC=8,AC=6,动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动,同时点P从A点开始在线段AC上以每秒1个单位长度的速度向点C移动.当一点停止运动,另一点也随之停止运动.设点Q,P移动的时间为t秒.当t=____________ 秒时△APQ与△ABC相似.
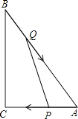
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com