
分析 分底为6和腰为6两种情况考虑:底为6时,则方程有两个相等的实数根,利用根的判别式△=0即可求出m的值;腰为6时,将x=6代入原方程求出m的值.综上即可得出结论.
解答 解:当底为6时,另两边为腰,即方程x2-(m+2)x+2m+4=0有两个相等的实数根,
∴△=[-(m+2)]2-4×1×(2m+4)=0,
解得:m=6或m=-2,
当m=-2时,方程x2-(m+2)x+2m+4=0的两个根为0,不符合题意,
当m=6时,原方程为x2-8x+16=(x-4)2=0,
此时方程的两个根为4,
∵4,4,6能为三角形的三条边,
∴m=6成立;
当腰为6时,将x=6代入x2-(m+2)x+2m+4=0中,
得:36-6(m+2)+2(m+2)=0,
解得:m=7,
当m=7时,原方程为x2-9x+18=(x-3)(x-6)=0,
解得:x=3,或x=6,
∵3,6,6能为三角形的三条边,
∴m=7成立.
综上可知:m的值为6或7.
点评 本题考查了根的判别式、一元二次方程的解以及等腰三角形的性质,解题的关键是分底为6和腰为6两种情况考虑.本题属于基础题,难度不大,解决该题型题目时,根据等腰三角形边的性质分情况讨论是关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
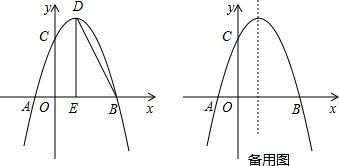
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
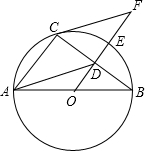 如图,AB为圆O的直径,点C、E在圆上,且点E是弧BC的中点,OE交弦BC于点D,点F在OE的延长线上,且∠BCF=∠BAC,BC=8,DE=2.
如图,AB为圆O的直径,点C、E在圆上,且点E是弧BC的中点,OE交弦BC于点D,点F在OE的延长线上,且∠BCF=∠BAC,BC=8,DE=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$,$\sqrt{12}$,$\sqrt{13}$ | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 3,4,5 | D. | 6,8,10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
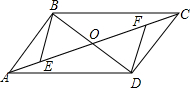 如图,?ABCD的对角线AC、BD相交于点O,OE=OF.
如图,?ABCD的对角线AC、BD相交于点O,OE=OF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com