
如图,在 OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(1)填空:点C的坐标是(______,______),对角线OB的长度是_______cm;
(2)当a=1时,设△OPQ的面积为S,求S与t的函数关系式,并直接写出当t为何值时,S的值最大?
(3)当点P在OA边上,点Q在CB边上时,线段PQ与对角线OB交于点M.若以O、M、P为顶点的三角形与△OAB相似,求a与t的函数关系式,并直接写出t的取值范围.

(1)C(2,2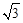 ),OB=4
),OB=4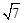 cm(2)
cm(2)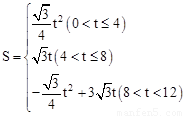 ,当t=8时,S最大(3)a=1+
,当t=8时,S最大(3)a=1+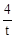 (0<t≤8)或a=1-
(0<t≤8)或a=1-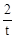 (6≤t≤8)
(6≤t≤8)
【解析】解:(1)C(2,2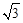 ),OB=4
),OB=4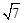 cm。
cm。
(2)①当0<t≤4时,
过点Q作QD⊥x轴于点D(如图1),
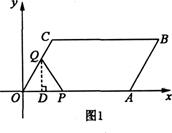
则QD=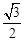 t。
t。
∴S=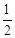 OP·QD=
OP·QD= t2。
t2。
②当4<t≤8时,
作QE⊥x轴于点E(如图2),
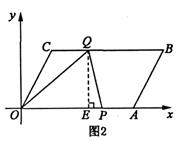
则QE=2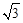 。
。
∴S =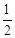 DP·QE=
DP·QE=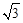 t。
t。
③当8<t<12时,
延长QP交x轴于点F,过点P作PH⊥AF于点H(如图3)。
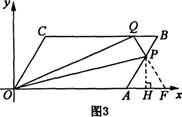
易证△PBQ与△PAF均为等边三角形,
∴OF=OA+AP=t,AP=t-8。∴PH=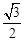 (t-8)。
(t-8)。
∴ =
=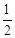 t·2
t·2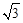 -
-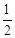 t·
t·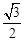 (t-8)
(t-8)
=- t2+3
t2+3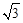 t。
t。
综上所述, 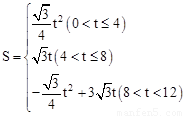 。
。
∵①②中S随t的增加而增加,
③中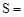
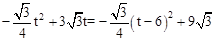 ,S随t的增加而减小,
,S随t的增加而减小,
∴当t=8时,S最大。
(3)①当△OPM∽△OAB时(如图4),
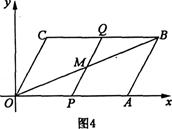
则PQ∥AB。
∴CQ=OP。
∴at-4=t,即a=1+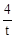 。 t的取值范围是0<t≤8。
。 t的取值范围是0<t≤8。
②当△OPM∽△OBA时(如图5),
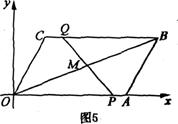
则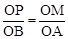 , 即
, 即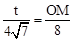 。∴OM=
。∴OM=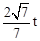 。
。
又∵QB∥OP,∴△BQM~△OPM。
∴ ,即
,即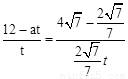 。
。
整理得t-at=2,即a=1-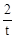 ,t的取值范围是6≤t≤8。
,t的取值范围是6≤t≤8。
综上所述:a=1+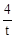 (0<t≤8)或a=1-
(0<t≤8)或a=1-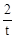 (6≤t≤8)。
(6≤t≤8)。
(1)如图,过点C、B分别作x的垂线于点M、N,
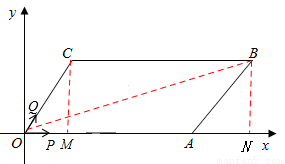
则在Rt△COM中,由∠AOC=60o,OC=4,应用锐角三角函数定义,可求得OM=2,CM=2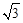 ,
,
∴
C(2,2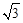 )。
)。
由CMNB是矩形和OA=8得BM=2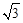 ,
,
ON=10,在Rt△OBN中,由勾股定理,得OB=4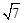 。
。
(2)分0<t≤4,4<t≤8和8<t<12分别讨论,得到函数关系式后根据一次函数和二次函数的性质求出S最大时t的值。
(3)分△OPM∽△OAB和△OPM∽△OBA两种情况讨论即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.| 3 |
| 3 |
| 7 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式:
如图,在?OABC中,O(0,0),A(2,2),C(4,0),写出一个能将该平行四边形分成面积相等的两部分的直线的解析式:| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(福建漳州卷)数学(带解析) 题型:解答题
如图,在 OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
OABC中,点A在x轴上,∠AOC=60o,OC=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(1)填空:点C的坐标是(______,______),对角线OB的长度是_______cm;
(2)当a=1时,设△OPQ的面积为S,求S与t的函数关系式,并直接写出当t为何值时,S的值最大?
(3)当点P在OA边上,点Q在CB边上时,线段PQ与对角线OB交于点M.若以O、M、P为顶点的三角形与△OAB相似,求a与t的函数关系式,并直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com