
【题目】如图,在Rt![]() 中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt
中,∠C=90°,AC=BC,在线段CB延长线上取一点P,以AP为直角边,点P为直角顶点,在射线CB上方作等腰 Rt![]() , 过点D作DE⊥CB,垂足为点E.
, 过点D作DE⊥CB,垂足为点E.

(1) 依题意补全图形;
(2) 求证: AC=PE;
(3) 连接DB,并延长交AC的延长线于点F,用等式表示线段CF与AC的数量关系,并证明.
【答案】(1)见解析;(2)见解析;(3)AC=CF,见解析
【解析】
(1)根据描述作出图形;
(2)先证明△ACP≌△DEP,根据全等的性质即可得出结论;
(3)根据(2)中全等得出PC=DE,再由线段间的转化可得出PC=BE,故可得出△DBE为等腰直角三角形,从而△BCF也为等腰直角三角形,结论得证.
解:(1)依题意补全图形;
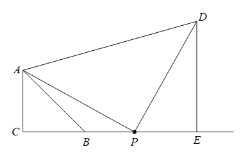
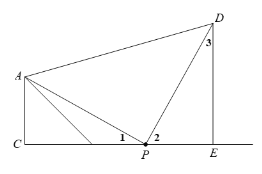
(2) 证明:∵DE⊥CB, ∠C=90°,
∴∠DEP=∠C =90°,
∴∠3+∠2=90°,
又∵∠APD =90°,
∴∠1+∠2=90°,
∴∠1=∠3,
又∵AP=DP,
∴△ACP≌△PED (AAS),
∴AC=PE.
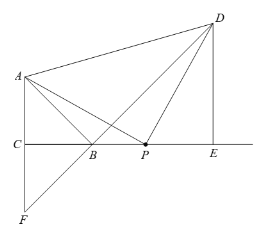
(3) 线段CF与AC的数量关系是CF=AC.
∵△ACP≌△PED,
∴PC=DE,
又∵AC=BC,
∴BC=PE, ∴PC=BE,
∴BE=DE,
即△DBE为等腰直角三角形,
易证△BCF为等腰直角三角形,
∴BC=CF,
∴AC=CF .


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列5个代数式:ac,a+b+c,4a﹣2b+c,2a+b,2a﹣b,其值大于0的个数为( )

A.3 B.2 C.5 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=1,有如下结论:
①c<1;
②2a+b=0;
③b2<4ac;
④若方程ax2+bx+c=0的两根为x1,x2,则x1+x2=2.

其中正确的结论是( )
A. ①② B. ①③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥BF.
(2)如图2所示,△ABC的顶点分别为A(﹣4,5),B(﹣3,2),C(4,﹣1)
①作出△ABC关于x轴对称的图形△A1B1C1;
②用三角板作出△ABC的AB边上的高CH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两个螺丝间的距离的最大值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线相交于O,且AC平分∠DAB.
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,试求点O到AB的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com