
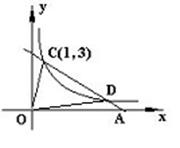
 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).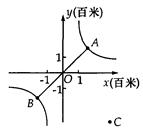
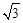 ,-2
,-2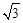 ) (2) 教练船没有最先赶到 理由略
) (2) 教练船没有最先赶到 理由略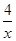 ,列方程组可求A、B两点坐标,在依题意判断△ABC为等边三角形,OA=2
,列方程组可求A、B两点坐标,在依题意判断△ABC为等边三角形,OA=2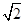 ,则OC=
,则OC=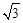 OA=2
OA=2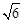 ,过C点作x轴的垂线CE,垂足为E,利用OC在第四象限的角平分线上求OE,CE,确定C点坐标;
,过C点作x轴的垂线CE,垂足为E,利用OC在第四象限的角平分线上求OE,CE,确定C点坐标;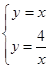 得
得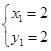 ,
,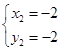
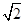 ,
,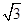 OA=2
OA=2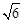 ,
,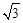 ,
,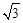 ,-2
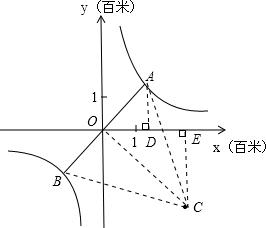
,-2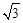 );
);
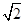 ,
,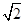 ,
,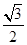 ?4
?4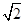 =2
=2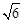 ,
,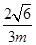 ,A、B两船所用时间均为
,A、B两船所用时间均为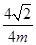 =
=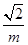 ,
,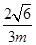 =
=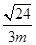 ,
,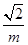 =
=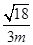 ,
,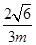 >
>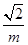 ;
;

科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
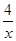 的图象与直线y=一
的图象与直线y=一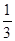 x的图象的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,△ABC的面积为
x的图象的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,△ABC的面积为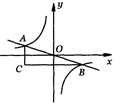
| A.8 | B.6 | C.4 | D.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com