
x2+![]() x+________=(x+________)2;2y2-3y+________=2(y-________)2.
x+________=(x+________)2;2y2-3y+________=2(y-________)2.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
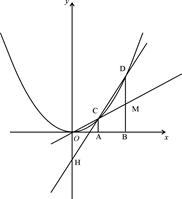
如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2的图象于点C和D,直线OC交BD于M,直线CD交y轴于点H。记C、D的横坐标分别为xC,xD,点H的纵坐标yH。
(1)证明:①S△CMD∶S梯形ABMC=2∶3
②xC·xD=-yH
(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD:S梯形ABMC=2∶3是否仍成立?请说明理由。
 (3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
 (3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。查看答案和解析>>
科目:初中数学 来源: 题型:
已知:m、n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图像经过点A(m,0)、B(0,n).
(1)求这个抛物线的解析式;
(2![]() )设(1)中抛物线与
)设(1)中抛物线与![]() 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2∶3的两部分,请求出P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com