
如图,抛物线y=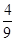 x2-
x2-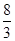 x-12与x轴交于A、C两点,与y轴交于B点.
x-12与x轴交于A、C两点,与y轴交于B点.
(1)求△AOB的外接圆的面积;
(2)若动点P从点A出发,以每秒2个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动。问当t为何值时,以A、P、Q为顶点的三角形与△OAB相似?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBAN面积的最大值.
(1)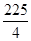 π;(2)t=
π;(2)t= ;(3)①不存在;②M(
;(3)①不存在;②M(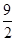 ,-6),
,-6),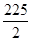
解析试题分析:(1)由题意得△AOB为直角三角形,分别求得抛物线y=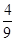 x2-
x2-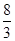 x-12与x轴、y轴的交点A、B的坐标,再根据勾股定理求得AB的长,最后根据直角三角形的性质即可求得结果;
x-12与x轴、y轴的交点A、B的坐标,再根据勾股定理求得AB的长,最后根据直角三角形的性质即可求得结果;
(2)由AP=2t,AQ=15-t,易求得AC=12,再分△APQ∽△AOB与△AQP∽△AOB两种情况根据相似三角形的性质即可求得结果;
(3)①先求得直线AB的函数关系式为y=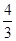 x-12,设点M的横坐标为x,则M(x,
x-12,设点M的横坐标为x,则M(x,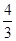 x-12),N(x,
x-12),N(x,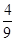 x2-
x2-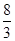 x-12),根据平行四边形的性质可得MN=OB=12,即可得到(
x-12),根据平行四边形的性质可得MN=OB=12,即可得到(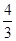 x-12)-(
x-12)-(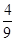 x2-
x2-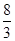 x-12)=12 ,而此方程的△<0,无实数根,故不存在这样的点M,使得四边形OMNB恰为平行四边形;
x-12)=12 ,而此方程的△<0,无实数根,故不存在这样的点M,使得四边形OMNB恰为平行四边形;
②由S四边形CBNA= S△ACB+ S△ABN="72+" S△ABN可得S△ABN=S△OBN+S△OAN-S△AOB=6x+(-2x2+12x+54)-54=-2x2+18x=-2(x-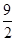 )2+
)2+ ,根据二次函数的性质即可求得结果.
,根据二次函数的性质即可求得结果.
(1)由题意得:A(9,0),B(0,-12)
∴OA=9,OB=12,
∴AB=15
∴S=π·(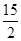 )2=
)2=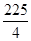 π;
π;
(2)AP=2t,AQ=15-t,易求AC=12,∴0≤t≤6
若△APQ∽△AOB,则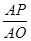 =
= .∴t=
.∴t= .
.
若△AQP∽△AOB,则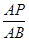 =
=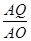 .∴t=
.∴t=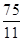 >6(舍去).
>6(舍去).
∴当t= 时,以A、P、Q为顶点的三角形与△OAB相似.
时,以A、P、Q为顶点的三角形与△OAB相似.
(3)直线AB的函数关系式为y=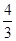 x-12.
x-12.
设点M的横坐标为x,则M(x,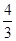 x-12),N(x,
x-12),N(x,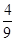 x2-
x2-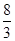 x-12).
x-12).
若四边形OMNB为平行四边形,则MN=OB=12
∴(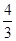 x-12)-(
x-12)-(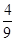 x2-
x2-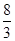 x-12)=12
x-12)=12
即x2-9x+27=0
∵△<0,
∴此方程无实数根,
∴不存在这样的点M,使得四边形OMNB恰为平行四边形;
②∵S四边形CBNA= S△ACB+ S△ABN="72+" S△ABN
∵S△AOB=54,S△OBN=6x,S△OAN= ·9·
·9·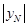 =-2x2+12x+54
=-2x2+12x+54
∴S△ABN=S△OBN+S△OAN-S△AOB=6x+(-2x2+12x+54)-54=-2x2+18x=-2(x-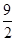 )2+
)2+
∴当x=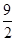 时,S△ABN最大值=
时,S△ABN最大值=
此时M(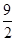 ,-6),S四边形CBNA最大=
,-6),S四边形CBNA最大=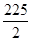 .
.
考点:二次函数的综合题
点评:本题知识点多,综合性强,难度较大,一般是中考压轴题,主要考查学生对二次函数的熟练掌握情况.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源:江苏中考真题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(带解析) 题型:填空题
如图,抛物线y= x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
(1)点Q的横坐标是 (用含t的代数式表示);
(2)若⊙P与⊙Q 相离,则t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市六校联谊中考模拟数学试卷(解析版) 题型:填空题
如图,抛物线y= x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .

(1)点Q的横坐标是 (用含t的代数式表示);
(2)若⊙P与⊙Q 相离,则t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省仪征市九年级上学期末考试数学试卷(解析版) 题型:解答题
如图,抛物线y=x2+bx+c与x轴交于点A、B(点A在点B左侧),与y轴交于点C(0,-3),且抛物线的对称轴是直线x=1.

(1)求b的值;
(2)点E是y轴上一动点,CE的垂直平分线交y轴于点F,交抛物线于P、Q两点,且点P在第三象限.当线段PQ =  AB时,求点E的坐标;
AB时,求点E的坐标;
(3)若点M在射线CA上运动,过点M作MN⊥y轴,垂足为N,以M为圆心,MN为半径作⊙M,当⊙M与x轴相切时,求⊙M的半径.
查看答案和解析>>
科目:初中数学 来源:2012届江苏省苏州工业园区九年级上学期期中测试数学卷 题型:选择题
如图,抛物线y=x2+1与双曲线y= 的交点A的横坐标是1,则关于x的不等式
的交点A的横坐标是1,则关于x的不等式 +x2+1 < 0的解集是( ▲ )
+x2+1 < 0的解集是( ▲ )
A.x>1 B.x<−1 C.0<x<1 D.−1<x<0

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com