
分析 方法一:由“风凰”方程的定义,可知ax2+bx+c=0满足a+b+c=0,可得:当x=1时,有a+b+c=0.故问题可证明;
方法二:将c=-a-b代入原方程左边,再将方程左边因式分解即可.
解答 证明:方法一:∵ax2+bx+c=0(a≠0)是“风凰”方程,
∴a+b+c=0,即a×12+b×1+c=0,
∴1必是该方程的一个根;
方法二:∵ax2+bx+c=0(a≠0)是“风凰”方程,
∴a+b+c=0,
∴c=-a-b,
原方程化为ax2+bx-a-b=0,
即a(x+1)(x-1)+b(x-1)=0,
∴(x-1)(ax+a+b)=0,
∴1必是该方程的一个根.
点评 本题考查了一元二次方程的解的定义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了因式分解法解一元二次方程.


科目:初中数学 来源: 题型:选择题
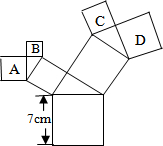 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为( )cm2.| A. | 3cm2 | B. | 4cm2 | C. | 7cm2 | D. | 49cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
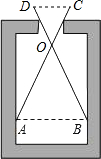 如图,用一个交叉卡钳(OA=OB,OC=OD)测量零件的内孔直径AB,若OC:OA=1:2,且量的CD=12mm,则零件的内孔直径AB是24mm.
如图,用一个交叉卡钳(OA=OB,OC=OD)测量零件的内孔直径AB,若OC:OA=1:2,且量的CD=12mm,则零件的内孔直径AB是24mm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
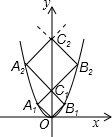 如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )
如图,已知点A1,A2,…,A2014在函数y=x2位于第二象限的图象上,点B1,B2,…,B2014在函数y=x2位于第一象限的图象上,点C1,C2,…,C2014在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2013A2014C2014B2014都是正方形,则正方形C2013A2014C2014B2014的边长为( )| A. | 2013 | B. | 2014 | C. | 2013$\sqrt{2}$ | D. | 2014$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com