
| k |
| x |
| 2 |
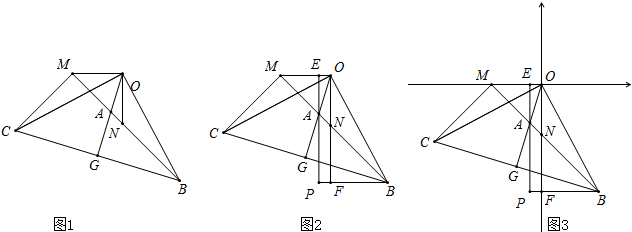
 (1)①证明:∵∠MON=∠BOC=90°,
(1)①证明:∵∠MON=∠BOC=90°,
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
| A、x2-10x+600=0 |
| B、x2+10x-600=0 |
| C、x(x-10)=600 |
| D、x(x+10)+600=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
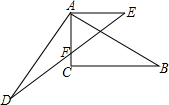 已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
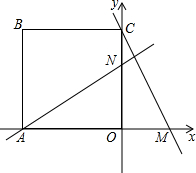 如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论:
如图,将边长为4的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x正半轴上运动,过A作直线MC的垂线交y轴于点N.下列结论:| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
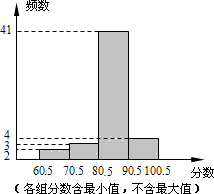 某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题:
某中学在一次健康知识测试中,抽取部分学生的成绩(分数为整数,满分100分)为样本,绘制成绩统计图如图所示,请结合统计图回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com