
分析 根据$\left\{\begin{array}{l}{a+b=8}\\{ab={c}^{2}-8\sqrt{2}c+48}\end{array}\right.$知a、b是方程x2-8x+c2-8$\sqrt{2}$c+48=0,即(x-4)2+(c-4$\sqrt{2}$)2=0的两根,从而得出$\left\{\begin{array}{l}{a=b=4}\\{c=4\sqrt{2}}\end{array}\right.$,代入到方程bx2+cx-a=0求解即可.
解答 解:由题意可知$\left\{\begin{array}{l}{a+b=8}\\{ab={c}^{2}-8\sqrt{2}c+48}\end{array}\right.$,
∴可令a、b是方程x2-8x+c2-8$\sqrt{2}$c+48=0的两根,
∴(x-4)2+(c-4$\sqrt{2}$)2=0,
∴$\left\{\begin{array}{l}{x-4=0}\\{c-4\sqrt{2}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=4}\\{c=4\sqrt{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{a=b=4}\\{c=4\sqrt{2}}\end{array}\right.$,
∴bx2+cx-a=0可化为4x2+4$\sqrt{2}$x-4=0,即x2+$\sqrt{2}$x-1=0,
解得:x1=$\frac{-\sqrt{2}+\sqrt{6}}{2}$,x2=$\frac{-\sqrt{2}-\sqrt{6}}{2}$.
故答案为:x1=$\frac{-\sqrt{2}+\sqrt{6}}{2}$,x2=$\frac{-\sqrt{2}-\sqrt{6}}{2}$.
点评 本题考查根与系数的关系,关键是先构造方程,然后根据非负数性质求出a、b、c的之后再进行求解.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
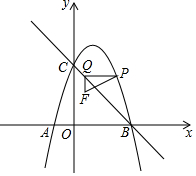 如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线的第一象限图象上运动.过点P作y轴的垂线与直线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1,设线段PQ的长度为d,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于点A、B两点,与y轴交于点C,且点B的坐标为(3,0),点P在这条抛物线的第一象限图象上运动.过点P作y轴的垂线与直线BC交于点Q,以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1,设线段PQ的长度为d,点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小南、小铭和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.
小南、小铭和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填补下列证明推理的理由
填补下列证明推理的理由查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com