Question

18．如图，在平面直角坐标系中，平行四边形OABC的顶点A在x轴上，顶点B的坐标为（4，6），直线y=kx+3k将平行四边形OABC分割成面积相等的两部分，则k的值是（　　）

• A． $\frac{3}{5}$
• B． $\frac{5}{3}$
• C． -$\frac{3}{5}$
• D． -$\frac{5}{3}$

Answer 1

分析 经过平行四边形对角线的交点的直线平分平行四边形的面积，故先求出对角线的交点坐标，再代入直线解析式求解．

解答 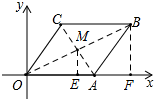解：如图，连接OB和AC交于点M，过点M作ME⊥x轴于点E，过点B作CB⊥x轴于点F，
∵四边形ABCD为平行四边形，
∴ME=$\frac{1}{2}$BF=3，OE=$\frac{1}{2}$OF=2，
∴点M的坐标为（2，3），
∵直线y=kx+3k将?ABCO分割成面积相等的两部分，
∴该直线过点M，
∴3=2k+3k，
∴k=$\frac{3}{5}$．
故选A．

点评 本题主要考查了平行四边形的性质以及一次函数图象上点的坐标特征，解题关键在于经过平行四边形对角线的交点的直线平分平行四边形的面积．