
分析 (1)方程利用配方法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)方程整理得:x2-2x=$\frac{1}{2}$,
配方得:x2-2x+1=$\frac{3}{2}$,即(x-1)2=$\frac{3}{2}$,
开方得:x-1=±$\frac{\sqrt{6}}{2}$,
解得:x1=1+$\frac{\sqrt{6}}{2}$,x2=1-$\frac{\sqrt{6}}{2}$;
(2)$\left\{\begin{array}{l}{2x+3y=1①}\\{x-2y=4②}\end{array}\right.$,
①-②×2得:7y=-7,即y=-1,
把y=-1代入②得:x=2,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,以及解一元二次方程-配方法,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
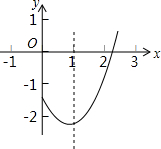 在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0.
在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
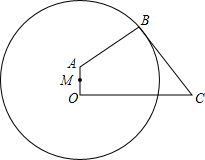 如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.
如图,为了保护运河入江口的古桥OA,规划建一座新桥BC,已知,古桥OA与河岸OC垂足,新桥BC与河岸AB垂直,且BC=AB,OC=210m,tan∠BCO=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a3•a4=a12 | B. | 2$\sqrt{2}$×$\sqrt{2}$=4 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
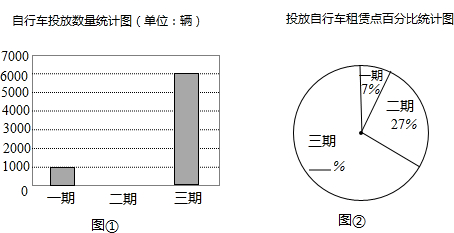
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com