
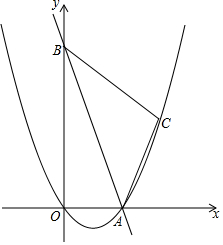
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+10��x�ᡢy���ཻ��A��B���㣬��C�������ǣ�8��4��������AC��BC��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+10��x�ᡢy���ཻ��A��B���㣬��C�������ǣ�8��4��������AC��BC������ ��1�������������ϵ���ص�ȷ������A��B���꣬�����ô���ϵ�������ɵó����ۣ�
��2�����AB2��AC2��BC2�������ù��ɶ����涨�����ɵó����ۣ�
��3���ȸ��ݹ��ɶ����ó�PA2=4t2+25��QA2=��10-t��2+52����������������⼴�ɣ�
��� �⣺��1�����O��A��C����������߽���ʽΪy=ax2+bx+c��
��ֱ��y=-2x+10��x�ᣬy���ཻ��A��B���㣬
���A��5��0���͵�B��0��10����
�֡�C������Ϊ��8��4����
��O��A��C������������߽���ʽΪy=ax2+bx+c��$\left\{\begin{array}{l}{c=0}\\{25a+5b+c=0}\\{64a+8b+c=4}\end{array}\right.$��
���a=$\frac{1}{6}$��b=-$\frac{5}{6}$��c=0��
�����������߽���ʽΪy=$\frac{1}{6}$x2-$\frac{5}{6}$x��
��2��ֱ�������Σ�
���ɣ���ͼ��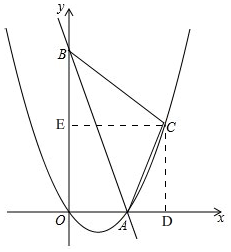 ��A��B����������OA=5��OB=10��
��A��B����������OA=5��OB=10��
�ɹ��ɶ�����AB2=OA2+OB2��
��AB2=125��
��C����CD��x����D����CE��y����E��
��C��������8��4����
��CD=4��CE=8��BE=10-4=6��AD=8-5=3��
�ɹ��ɶ�����AC2=CD2+AD2=42+32=25��
��AC=5��
��BC2=BE2+CE2=62+82=100��
��BC2+AC2=100+25=AB2��
���ɹ��ɶ����á�ACB=90�㣮
���ABC��ֱ�������Σ�
��3��������ö����˶�t���OP=2t��BQ=t��CQ=10-t��
�ɹ��ɶ�����PA2=OP2+OA2=4t2+25��QA2=QC2+AC2=��10-t��2+52��
��PA=QA��
��PA2=QA2��
��4t2+25=��10-t��2+52��
���t1=$\frac{10}{3}$��t2=-10������ȥ����
�ද���˶�$\frac{10}{3}$��ʱ��PA=QA��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ���������ɶ������涨�������̵�˼�룬�⣨1���Ĺؼ������ô���ϵ������������߽���ʽ���⣨2���Ĺؼ������AB2��AC2��BC2���⣨3���ؼ��DZ�ʾ��PA2=4t2+25��QA2=��10-t��2+52��


 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
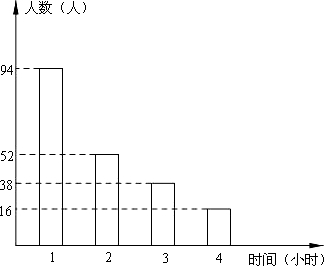 ij�С�ÿ�����һСʱ���Ҹ�����һ���ӡ���ѿ�չ��һ�꣬Ϊ�˽���д����Ŀ�չ�����ij����ͳ�ƹ�˾���������µ��鷽ʽ�е�һ�ֽ��е��飺A����һ���������ѡȡ200������B����һ������IJ�ͬסլ¥�����ѡȡ200������C���Ӹ��й����ֻ��������������ȡ200�����������Ϊ�������Ȼ����е��飮
ij�С�ÿ�����һСʱ���Ҹ�����һ���ӡ���ѿ�չ��һ�꣬Ϊ�˽���д����Ŀ�չ�����ij����ͳ�ƹ�˾���������µ��鷽ʽ�е�һ�ֽ��е��飺A����һ���������ѡȡ200������B����һ������IJ�ͬסլ¥�����ѡȡ200������C���Ӹ��й����ֻ��������������ȡ200�����������Ϊ�������Ȼ����е��飮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
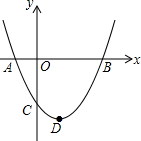 ��ͼ�����κ���y=ax2+bx+c��a��0��ͼ��Ķ���ΪD����ͼ����x��Ľ���A��B�ĺ�����ֱ�Ϊ-1��3����y�Ḻ���ύ�ڵ�C����������������У�
��ͼ�����κ���y=ax2+bx+c��a��0��ͼ��Ķ���ΪD����ͼ����x��Ľ���A��B�ĺ�����ֱ�Ϊ-1��3����y�Ḻ���ύ�ڵ�C����������������У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
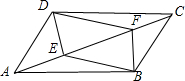 ��֪����ͼ���ı���ABCDΪƽ���ı��Σ�E��F�ǶԽ���AC�ϵ����㣬AE=CF������DE��BE��BF����֤���ı���DEBF��ƽ���ı��Σ�
��֪����ͼ���ı���ABCDΪƽ���ı��Σ�E��F�ǶԽ���AC�ϵ����㣬AE=CF������DE��BE��BF����֤���ı���DEBF��ƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com