
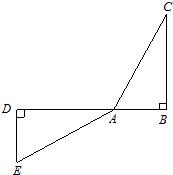
 15、两个全等的三角形如下图所示放置,点B、A、D在同一直线上.操作:在图中,在CB边上截取CM=AB,连接DM,交AC于N.请探究∠AND的大小,并证明你的结论.
15、两个全等的三角形如下图所示放置,点B、A、D在同一直线上.操作:在图中,在CB边上截取CM=AB,连接DM,交AC于N.请探究∠AND的大小,并证明你的结论. 解:作图基本正确,确定M,连接DM,确定交点N
解:作图基本正确,确定M,连接DM,确定交点N

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2009年北京市崇文区初三二模数学试题 题型:059
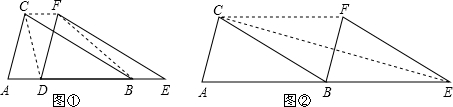
两个全等的三角形ABC和DEF重叠在一起,△ABC的面积为3,且AB=CB.固定△ABC不动,将△DEF进行如下操作:
(1)如图,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积;

(2)如图,当D点B向右平移到B点时,试判断CE与BF的位置关系,并说明理由;

(3)在(2)的条件下,若∠AEC=15°,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:北京模拟题 题型:解答题
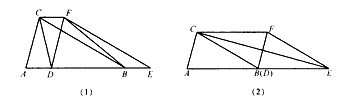
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com