
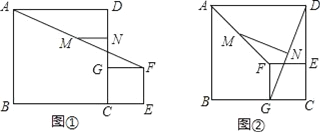
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
【答案】 MN=![]() DG,MN⊥DG; (1)的结论仍然成立.
DG,MN⊥DG; (1)的结论仍然成立.
【解析】(1)连接FN并延长,与AD交于点S,如图①,易证△SDN≌△FGN,则有DS=GF,SN=FN,然后运用三角形中位线定理就可解决问题;
(2)过点M作MT⊥DC于T,过点M作MR⊥BC于R,连接FC、MD、MG,如图②,根据平行线分线段成比例可得BR=GR=![]() BG,DT=ET=
BG,DT=ET=![]() DE,根据梯形中位线定理可得MR=
DE,根据梯形中位线定理可得MR=![]() (FG+AB),MT=
(FG+AB),MT=![]() (EF+AD),从而可得MR=MT,RG=TD,由此可得△MRG≌△MTD,则有MG=MD,∠RMG=∠TMD,则有∠RMT=∠GMD,进而可证到△DMG是等腰直角三角形,然后根据等腰三角形的性质和直角三角形斜边上的中线等于斜边的一半,就可解决问题;
(EF+AD),从而可得MR=MT,RG=TD,由此可得△MRG≌△MTD,则有MG=MD,∠RMG=∠TMD,则有∠RMT=∠GMD,进而可证到△DMG是等腰直角三角形,然后根据等腰三角形的性质和直角三角形斜边上的中线等于斜边的一半,就可解决问题;
(3)连接GM到点P,使得PM=GM,延长GF、AD交于点Q,连接AP,DP,DM如图③,易证△APD≌△CGD,则有PD=DG,根据等腰三角形的性质可得DM⊥PG,根据直角三角形斜边上的中线等于斜边的一半可得MN=![]() DG.要求MN的最大值和最小值,只需求DG的最大值和最小值,由GC=CE=3可知点G在以点C为圆心,3为半径的圆上,再由DC=BC=7,就可求出DG的最大值和最小值.
DG.要求MN的最大值和最小值,只需求DG的最大值和最小值,由GC=CE=3可知点G在以点C为圆心,3为半径的圆上,再由DC=BC=7,就可求出DG的最大值和最小值.
解:(1)连接FN并延长,与AD交于点S,如图①.
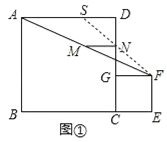
∵四边形ABCD和四边形EFGC都是正方形,
∴∠D=90°,AD=DC,GC=GF,AD∥BE∥GF,
∴∠DSN=∠GFN.
在△SDN和△FGN中,
∠DSN=∠GFN,∠SND=∠FNG,DN=GN,,
∴△SDN≌△FGN,
∴DS=GF,SN=FN.
∵AM=FM,
∴MN∥AS,MN=![]() AS,
AS,
∴∠MNG=∠D=90°,
MN=![]() (AD﹣DS)=
(AD﹣DS)=![]() (DC﹣GF)=
(DC﹣GF)=![]() (DC﹣GC)=
(DC﹣GC)=![]() DG.
DG.
故答案为MN=![]() DG,MN⊥DG;
DG,MN⊥DG;
(2)(1)的结论仍然成立.
理由:过点M作MT⊥DC于T,过点M作MR⊥BC于R,连接FC、MD、MG,如图②,
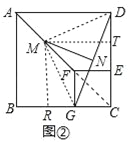
则A、F、C共线,MR∥FG∥AB,MT∥EF∥AD.
∵AM=FM,
∴BR=GR=![]() BG,DT=ET=
BG,DT=ET=![]() DE,
DE,
∴MR=![]() (FG+AB),MT=
(FG+AB),MT=![]() (EF+AD).
(EF+AD).
∵四边形ABCD和四边形EFGC都是正方形,
∴FG=GC=EC=EF,AB=BC=DC=AD,
∴MR=MT,RG=TD.
在△MRG和△MTD中,
MR=MT,∠MRG=∠MTD,RG=TD,
∴△MRG≌△MTD,
∴MG=MD,∠RMG=∠TMD,
∴∠RMT=∠GMD.
∵∠MRC=∠RCT=∠MTC=90°,
∴四边形MRCT是矩形,
∴∠RMT=90°,
∴∠GMD=90°.
∵MG=MD,∠GMD=90°,DN=GN,
∴MN⊥DG,MN=![]() DG.
DG.
(3)延长GM到点P,使得PM=GM,延长GF、AD交于点Q,连接AP,DP,DM如图③,
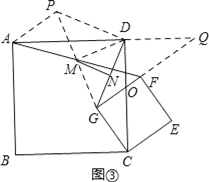
在△AMP和△FMG中,
AM=FM,∠AMP=∠FMG,PM=GM,
∴△AMP≌△FMG,
∴AP=FG,∠APM=∠FGM,
∴AP∥GF,
∴∠PAQ=∠Q,
∵∠DOG=∠ODQ+∠Q=∠OGC+∠GCO,
∠ODQ=∠OGC=90°,
∴Q=∠GCO,
∴∠PAQ=∠GCO.
∵四边形ABCD和四边形EFGC都是正方形,
∴DA=DC,GF=GC,
∴AP=CG.
在△APD和△CGD中,
AP=CG,∠PAD=∠GCD,AD=CD,
∴△APD≌△CGD,
∴PD=DG.
∵PM=GM,
∴DM⊥PG.
∵DN=GN,
∴MN=![]() DG.
DG.
∵GC=CE=3,
∴点G在以点C为圆心,3为半径的圆上,
∵DC=BC=7,
∴DG的最大值为7+3=10,最小值为7﹣3=4,
∴MN的最大值为5,最小值为2.
“点睛”本题主要考查了全等三角形的判定与性质、正方形的性质、三角形中位线定理、平行线分阶段成比例、梯形中位线定理、等腰直角三角形的判定与性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、圆的定义、平行线的判定与性质等知识,综合性强,有一定的难度,证到△DMG是等腰直角三角形是解决第(2)小题的关键,证到MN=![]() DG是解决第(3)小题的关键.
DG是解决第(3)小题的关键.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=60°,DE是斜边AC的中垂线,分别交AB,AC于D,E两点.若BD=2,则AC的长是( )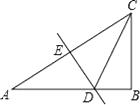
A.4
B.4 ![]()
C.8
D.8 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
(1)求证:GC是⊙F的切线;
(2)填空:
①若∠BAD=45°,AB=2![]() ,则△CDG的面积为_____.
,则△CDG的面积为_____.
②当∠GCD的度数为_____时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是等腰梯形,∠ABC=60°,若其四边满足长度的众数为5,平均数为 ![]() ,上、下底之比为1:2,则BD的长是( ).
,上、下底之比为1:2,则BD的长是( ).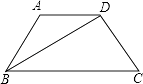
A.5
B.5 ![]()
C.3 ![]()
D.3 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com