
����Ŀ���������Ϊ��������ء����к��о�������Ȼ�������Ļ��Ų�ʵ��ij���������ڵ�Ŀ����Ϊ�����ṩ֪ʶ�����������ͷ���.�����������ǵ������ѧϰ�ι۵�����Խ��Խ��.2012-2018���ҹ�����ݲι�����ͳ������:
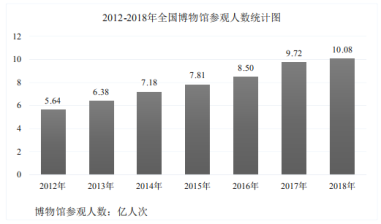
С���о������ͳ��ͼ���ó��ĸ�����:��2012�굽2018�꣬�ҹ�����ݲι�����������������2019��ĩ�ҹ�����ݲι��������ƽ��ﵽ10.82���˴Σ���2012�굽2018�꣬�ҹ�����ݲι�����������������2017�ꣻ��2016�굽2018�꣬�ҹ�����ݲι�����ƽ���������ʳ���10��.������ȷ���ǣ� ��
A.�٢�B.�٢ڢ�C.�٢ڢ�D.�٢ڢۢ�
���𰸡�A
��������
��������ͳ��ͼ�е���Ϣ��4�����۽����жϼ��ɣ�
������ͳ��ͼ��֪����2012�굽2018�꣬����ݲι��������ֳ�������̬�ƣ��ʢ���ȷ��
��2012�굽2018��������10.08-5.64=4.44�����˴Σ���ƽ��ÿ������4.44��6=0.74�����˴Σ�
��2019�꽫��ﵽ10.08+0.74=10.82�����˴Σ����ʢ���ȷ��
2013��������6.34-5.64=0.7�����˴Σ���2014��������7.18-6.34=0.84�����˴Σ���2015��������7.81-7.18=0.63�����˴Σ���2016��������8.50-7.81=0.69�����˴Σ���2017��������9.72-8.50=1.22�����˴Σ���2018��������10.08-9.72=0.36�����˴Σ�����2017��������ʢ���ȷ��
���2016�굽2018����ƽ��������Ϊx����8.50��1+x��2=10.08
���x![]() 0.09����ֵ���ᣩ������ƽ������ԼΪ9%���ʢܴ���
0.09����ֵ���ᣩ������ƽ������ԼΪ9%���ʢܴ���
���Ͽɵ���ȷ���Ǣ٢ڢ�.
��ѡ��B.


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�OΪ����ABCD�ĶԳ����ģ���֪C��2��0����D��0����1����NΪ�߶�CD��һ�㣨����C��D�غϣ���
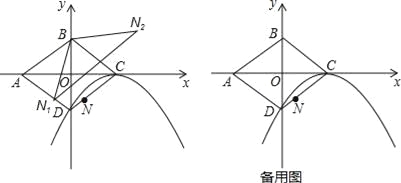
��1������CΪ���㣬�Ҿ�����D�������߽���ʽ��
��2����N����BD�ĶԳƵ�ΪN1��N����BC�ĶԳƵ�ΪN2����֤����N1BN2�ס�ABC��
��3����2����N1N2����Сֵ��
��4������N��y���ƽ���߽���1���е��������ڵ�P����QΪֱ��AB�ϵ�һ�����㣬����PQA=��BAC����PQ��Сʱ��Q���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=![]() x-3�뷴��������y=
x-3�뷴��������y=![]() ��ͼ���ཻ�ڵ�A��4��n������x���ཻ�ڵ�B��
��ͼ���ཻ�ڵ�A��4��n������x���ཻ�ڵ�B��

��1����գ�n��ֵΪ ��k��ֵΪ ��
��2����ABΪ��������ABCD��ʹ��C��x���������ϣ���D�ڵ�һ���ޣ����D�����ꣻ
��3���۲췴�Ⱥ���y=![]() ��ͼ��y��-2ʱ����ֱ��д���Ա���x��ȡֵ��Χ��
��ͼ��y��-2ʱ����ֱ��д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����A��B���ּ�������100����Ҫ��A�ּ���������������B�ֵ�![]() ���Ҳ�����B�ֵ�
���Ҳ�����B�ֵ�![]() ����֪A��B���ּ������ĵ��۷ֱ���150Ԫ/����100Ԫ/�����蹺��A�ּ�����x����
����֪A��B���ּ������ĵ��۷ֱ���150Ԫ/����100Ԫ/�����蹺��A�ּ�����x����
��1����ƻ����������ּ������������y��Ԫ����x�ĺ�����ϵʽ��
��2���ʸù�˾���ƻ����������ּ������ж����ַ�����
��3�������г����鲨����ʵ�ʹ���ʱ��A�ּ����������µ���3m��m��0��Ԫ/����ͬʱB�ּ����������ϵ���2mԪ/������ʱ���������ּ������������ٷ���Ϊ12150Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣨д��������̣�
��1��(-35) + 18 + (-5) + (+22)
��2��![]()
��3��![]()
��4��![]()
��5��![]()
��6��9��5��(��3)��(��2)2��4
��7��(-22)��(-3)2+(-32)��4;
��8����32+1��4��![]() ��|��1
��|��1![]() |������0.5��2
|������0.5��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�ͳ���˽���1��5��A��B����Ʒ�Ʊ�������������������õ����ݻ��Ƴ�����ͳ��ͼ
��1�����̳����ʱ����A.B����Ʒ�Ʊ���������������λ���ֱ�Ϊ �� ��
��2����������Ʒ�����������ķ���Ƚϲ�˵�����̳�1��5��������Ʒ�Ʊ��������������ȶ��ԣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��1�������������ϲ���Ŀ�����Ŀ����ȫ��ѧ�����е��飨ÿ��ѧ���ֱ�ѡһ�����Ŀ���������ݵ������г�ͳ�Ʊ������Ƴ�����ͳ��ͼ��

����������Ϣ����������⣺
��1��![]() ��
��![]() ��
��
��2������ͳ��ͼ�л�������Ŀ����Ӧ���ε�Բ�ĽǶ���Ϊ ![]() ��
��
��3����ѡ��ģ��Ŀ��![]() ��ѧ�������ѡȡ
��ѧ�������ѡȡ![]() ��ѧ���μ�ѧУ��ģ��ȤС��ѵ���������оٷ�������״ͼ���б�������ѡȡ��
��ѧ���μ�ѧУ��ģ��ȤС��ѵ���������оٷ�������״ͼ���б�������ѡȡ��![]() ��ѧ����ǡ����
��ѧ����ǡ����![]() ��������
��������![]() ��Ů���ĸ��ʣ�
��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ͼ�٣��ڵ���Rt![]() �У�
�У�![]() ,
,![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��
��һ�㣬��![]() Ϊ�뾶��
Ϊ�뾶��![]() ��
��![]() �ڵ�
�ڵ�![]() ,����
,����![]() ��
��![]() ���߶�
���߶�![]() ��
��![]() ��
��![]() ���е�ֱ�Ϊ
���е�ֱ�Ϊ![]() ��
��![]() ��
��![]() .
.
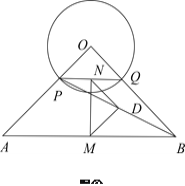
��1����̽��![]() ��ʲô���������Σ�˵�����ɣ�
��ʲô���������Σ�˵�����ɣ�
��2����![]() �Ƶ�
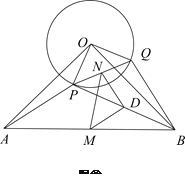
�Ƶ�![]() ��ʱ�뷽����ת��ͼ�ڵ�λ�ã����������Ƿ��������֤��������
��ʱ�뷽����ת��ͼ�ڵ�λ�ã����������Ƿ��������֤��������
��3����![]() ,��
,��![]() �Ƶ�
�Ƶ�![]() ��ƽ����������ת����
��ƽ����������ת����![]() �����y�����ֵ����Сֵ�IJ�.
�����y�����ֵ����Сֵ�IJ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
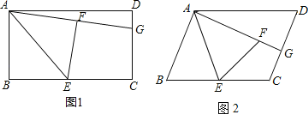
����Ŀ����1���������֣���ͼ1���ھ���ABCD�У�E��BC���е㣬����ABE��AE�۵���õ���AFE����F�ھ���ABCD�ڲ����ӳ�AF��CD�ڵ�G�������߶�GF��GC�к�������ϵ����֤����Ľ��ۣ�
��2����Ӧ�ã��ڣ�1���У����AB��4��AD��6����DG�ij���
��3�����̽������ͼ2������1���еľ���ABCD��Ϊƽ���ı��Σ������������䣬��1���еĽ����Ƿ���Ȼ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com