Question

平面内的两条直线有相交和平行两种位置关系（本题6分）

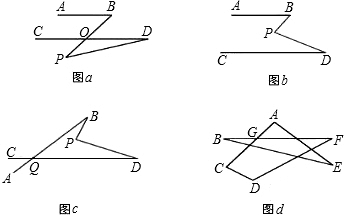
（1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B-∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请说明理由；

（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需说明理由）

（3）求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．（简述理由）

 

Answer 1

（1） 

   （2）

   （3）等于360° 

解析:本题利用三角形的外角定理和内角和定理。