
【题目】在平面直角坐标系![]() 中,
中,![]() 中的点
中的点![]() 是
是![]() 边上的一点,过点
边上的一点,过点![]() 的反比例函数
的反比例函数![]()
![]() 与
与![]() 边交于点
边交于点![]() ,连接
,连接![]() .
.
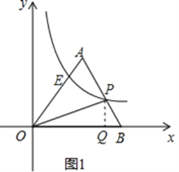
(1)如图1,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的面积为5,求直线
的面积为5,求直线![]() 和反比例函数
和反比例函数![]() 的解析式;
的解析式;
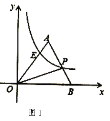
(2)如图2,若![]() ,过
,过![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,并且
,并且![]() 的面积为
的面积为![]() ,求反比例函数
,求反比例函数![]() 的解析式及点
的解析式及点![]() 的坐标.
的坐标.
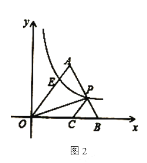
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ,见解析.
,见解析.
【解析】
(1)过点P作PQ⊥x轴交x轴于点Q,利用待定系数法求出直线AB的解析式,根据△OPB的面积为5求出PQ的长,代入直线AB的解析式可得出P点坐标,进而可得出反比例函数的解析式;
(2)过点E作EF⊥x轴交x轴于点F,过点P作PS⊥x轴交x轴于点S,利用锐角三角函数的定义求出OF及EF的长,故可得出反比例函数的解析式,根据△OPC的面积为![]() 求出OCPS的长,再由锐角三角函数的定义得出PS的长,进而可得出P点坐标.
求出OCPS的长,再由锐角三角函数的定义得出PS的长,进而可得出P点坐标.
解:(1)如图1,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
![]() 设直线
设直线![]() 的解析式为
的解析式为![]()
![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() ,且
,且![]() 的面积为5,
的面积为5,
![]()
![]() ,点
,点![]() 纵坐标为2.
纵坐标为2.
![]() 点
点![]() 在直线
在直线![]() 上
上![]() ,解得
,解得![]() .
.
![]() 点
点![]() 坐标为
坐标为![]()
![]() 此反比例函数的解析式为
此反比例函数的解析式为![]() ;
;
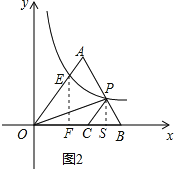
(2)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() ,
,
![]() 此反比例函数的解析式为
此反比例函数的解析式为![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 点
点![]() 坐标为
坐标为![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
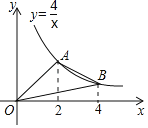
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)解方程:x4﹣5x2+4=0.
这是一个一元四次方程,根据该方程的特点,我们可以借助“换元法”将高次方程“降次”,进而解得未知数的值.
解:设 x2=y,那么 x4=y2,于是原方程可变为 y2﹣5y+4=0,解得 y1=1,y2=4. 当 y1=1 时,x2=1,x=±1;当 y2=4 时,x2=4,x=±2;
原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
(触类旁通)参照例题解方程:(x2+x)2﹣4(x2+x)﹣12=0;
(解决问题)已知实数 x,y 满足(2x+2y+3)(2x+2y﹣3)=27,求 x+y 的值;
(拓展迁移)分解因式:(x2+4x+3)(x2+4x+5)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 、
、![]() 为直线
为直线![]() 上的两动点,
上的两动点,![]() ,
,![]() ,
,![]() ;
;
(1)当点![]() 、
、![]() 重合,即
重合,即![]() 时(如图
时(如图![]() ),试求
),试求![]() .(用含
.(用含![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
(2)请直接应用(1)的结论解决下面问题:当![]() 、
、![]() 不重合,即
不重合,即![]() ,
,
①如图![]() 这种情况时,试求
这种情况时,试求![]() .(用含
.(用含![]() ,
,![]() ,
,![]() ,
,![]() 的代数式表示)
的代数式表示)
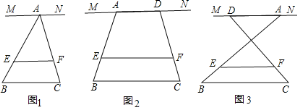
②如图![]() 这种情况时,试猜想
这种情况时,试猜想![]() 与
与![]() 、
、![]() 之间有何种数量关系?并证明你的猜想.
之间有何种数量关系?并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象经过点A (﹣2,6),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.

(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com