
【题目】定义:对于函数y,我们称函数叫做函数|y|的正值函数.例如:函数y![]() 的正值函数为y=|
的正值函数为y=|![]() |.
|.
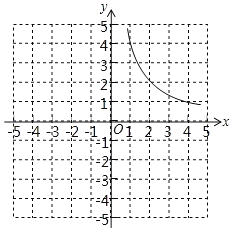
如图,曲线y![]() (x>0)请你在图中画出y=x+3的正值函数的图象.
(x>0)请你在图中画出y=x+3的正值函数的图象.
(1)写出y=x+3的正值函数的两条性质;
(2)y=x+3的正值函数的图象与x轴、y轴、曲线y![]() (x>0)的交点分别是A,B,C.点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与正值函数图象交于另一点E,与曲线交于点P.
(x>0)的交点分别是A,B,C.点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与正值函数图象交于另一点E,与曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
【答案】(1)①图象与x轴交于(﹣3,0),②当x<﹣3时,y随x的增大而减小;(2)①m![]() 时,△PAD的面积最大,最大值为
时,△PAD的面积最大,最大值为![]() ;②能,D(﹣1,2).
;②能,D(﹣1,2).
【解析】
(1)利用描点法画出y=x+3的正值函数为y=|x+3|的图形即可;
(2)①设D(m,m+3),则P(![]() ,m+3),利用三角形的面积公式构建二次函数,利用二次函数的性质解决问题即可;
,m+3),利用三角形的面积公式构建二次函数,利用二次函数的性质解决问题即可;
②如图2中,连接EC.假设四边形APCE是平行四边形,则AD=CD,求出点E,P的坐标,再验证是不是平行四边形即可.
(1)y=x+3的正值函数为y=|x+3|,函数图象如图所示:
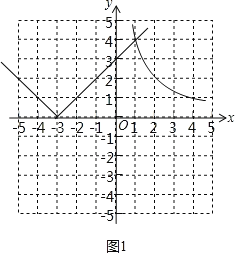
函数y=|x+3|的性质:①图象与x轴交于(﹣3,0).
②当x<﹣3时,y随x的增大而减小.
③当x>﹣3时,y随x的增大而增大.
(2)①如图2中,
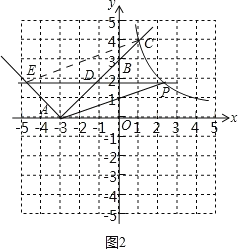
设D(m,m+3),则P(![]() ,m+3),
,m+3),
∴PD![]() m
m![]() ,
,
∴S△APD![]() (
(![]() )(m+3)
)(m+3)![]() (m2+3m﹣4)
(m2+3m﹣4)![]() (m
(m![]() )2
)2![]() ,
,
∵![]() 0,
0,
∴m![]() 时,△PAD的面积最大,最大值为
时,△PAD的面积最大,最大值为![]() .
.
②如图2中,连接EC.假设四边形APCE是平行四边形,则AD=CD.
∵A(﹣3,0),C(1,4),
∴D(﹣1,2),
∴P(2,2),E(﹣5,2),
∴DE=DP=3.
∵DE=DP,AD=DC,
∴四边形APCE是平行四边形,符合条件.
【点晴】
考查了反比例函数的性质、平行四边形的判定和性质等知识,解题的关键是理解题意,学会利用参数构建二次函数解决最值问题.


科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.

(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里,装有若干个完全相同的A、B、C三种球,其中A球x个,B球x个,C球(x+1)个.若从中任意摸出一个球是A球的概率为0.25.
(1)这个袋中A、B、C三种球各多少个?
(2)若小明从口袋中随机模出1个球后不放回,再随机摸出1个.请你用画树状图的方法求小明摸到1个A球和1个C球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个黑球和2个红球,这些球除颜色外都相同.顾客每次摸出一个球,若摸到黑球,则获得1份奖品;若摸到红球,则没有奖品.
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防范疫情,顺利复学,某市教育局决定从甲、乙两地用汽车向![]() 两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,
两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,![]() 两校分别需要口罩30万个,20万个,两地到
两校分别需要口罩30万个,20万个,两地到![]() 两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
路程 | 路程 | |
甲地 | 乙地 | |
A校 | 10 | 20 |
B校 | 15 | 15 |
(1)根据题意,在答题卡中填写下表:
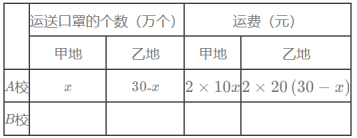
(2)设总运费为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
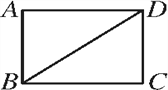
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
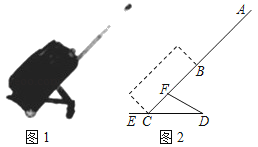
【题目】小红要外出参加一项庆祝活动,需网购一个拉杆箱,图1,图2分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,B,F在AC上,C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,求AC的长度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com