
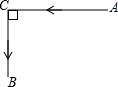
 甲船和乙船分别从A港和C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且A,C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都指直线距离,图中AC⊥CB.)
甲船和乙船分别从A港和C港同时出发,各沿图中箭头所指的方向航行(如图所示).现已知甲、乙两船的速度分别是16海里/时和12海里/时,且A,C两港之间的距离为10海里.问:经过多长时间,甲船和乙船之间的距离最短?最短距离为多少?(注:题中的“距离”都指直线距离,图中AC⊥CB.)
| (10-16x)2+(12x)2 |
| (20x-8)2+36 |
| 2 |
| 5 |
| 2 |
| 5 |


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
| A、三角形的外心是三角形三条高线的交点 |
| B、等腰三角形的外心一定在它的内部 |
| C、任何一个三角形有且仅有一个外接圆 |
| D、三角形的内心可能在它的外部 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 名字 | 票数临时记录 | 总票数/张 |
| 小华 |  |
|
| 小颖 |  |
|
| 小亮 |  |
|
| 小聪 |  |
查看答案和解析>>
科目:初中数学 来源: 题型:
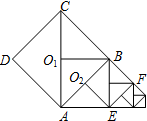 如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,如此作下去…则所作的第2013个正方形的面积是
如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,如此作下去…则所作的第2013个正方形的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com