已知∠ABC.点P在射线BA上.请根据“同位角相等.两直线平行 .利用直尺和圆规.过点P作直线PD平行于BC.(保留作图痕迹.不写作法.) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

已知∠ABC，点P在射线BA上，请根据“同位角相等，两直线平行”，利用直尺和圆规，过点P作直线PD平行于BC。（保留作图痕迹，不写作法。）

作图见解析.

解析试题分析：在AB的同侧作∠APD=∠B，则PD∥BC.
作图如下：第一步：

第二步：

第三步：

考点：作一个角等于已知角.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

已知：如图，AD∥BC，∠1=∠2。求证：∠3+∠4=180°。

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

某同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②．图①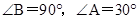中，；图②中，．图③是该同学所做的一个实验：他将△的直角边与△的斜边重合在一起，并将△沿方向移动．在移动过程中，两点始终在边上(移动开始时点与点重合)．
(1) 在△沿方向移动的过程中，该同学发现：两点间的距离；连接的度数．（填“不变”、“ 逐渐变大”或“逐渐变小”）
(2) △在移动过程中，与度数之和是否为定值，请加以说明；
(3) 能否将△移动至某位置，使的连线与平行？如果能，请求出此时的度数，如果不能，请说明理由。

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

填写推理理由（1×10=10分）
如图，已知AB∥CD ，∠1=∠2，∠3=∠4，试说明AD∥BE
解：∵AB∥CD（已知）
∴∠4=∠_____（               ）
∵∠3=∠4（已知）
∴∠3=∠_____（               ）
∵∠1=∠2（已知）
∴∠ CAE+     =∠CAE+
即 ∠_____ =∠_____
∴∠３＝∠_____
∴ＡＤ∥ＢＥ（                    ）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

补全下列各题解题过程．（6分）
如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证DF∥AC．
证明：∵∠1=∠2（已知）
∠2=∠3 ∠1=∠4 （       ）
∴∠3=∠4 （等量代换）
∴_DB__∥_____ (                         )
∴∠C=∠ABD      (                        )
∵∠C=∠D    ( 已知   )
∴∠D=∠ABD(                       )
∴DF∥AC(                              )