
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分![]() 交BC于点E,若
交BC于点E,若![]() ,
,
(1)求![]() 的度数。
的度数。
(2)求![]() 的度数。
的度数。
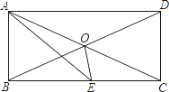
【答案】(1)∠ACB=30°;(2)∠BOE=75°;
【解析】
(1)由矩形的性质可得∠BAD=∠ABC=90°,由角平分线的定义可得∠BAE=45°,从而得∠AEB=45°,再根据三角形外角的性质即可求得答案;
(2)由矩形的性质可得AO=BO=OC,从而有∠OBC=∠OCB=30°,再证明△AOB是等边三角形,从而可得AB=OB,再根据∠BAE=∠AEB=45°,得到AB=BE,继而得BE=BO,再根据等腰三角形的性质即可求得答案.
(1)∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,
∵AE平分∠BAD,
∴∠BAE=45°,
∴∠AEB=90°-∠BAE=45°,
∵∠AEB=∠EAC+∠ACB,∠CAE=15°,
∴∠ACB=45°-15°=30°;
(2)∵四边形ABCD是矩形,
∴AO=CO=![]() AC,BO=
AC,BO=![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=OC,
∴∠OBC=∠OCB=30°,
∵∠BAO=∠BAE+∠CAE=45°+15°=60°
∴△AOB是等边三角形,
∴AB=OB,
∵∠BAE=∠AEB=45°,
∴AB=BE,
∴BE=BO,
∴∠BOE=(180°-30°)÷2=75°.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
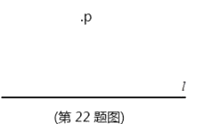
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外卖小哥骑车从商家出发,向东骑了3千米到达小林家,继续骑2.5千米到达小红家,然后向西骑了10千米到达小明家,最后返回商家。
(1)以商家为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小林家,小红家的位置。(小林家用点A表示,小红家用点B表示,小明家用点C表示)
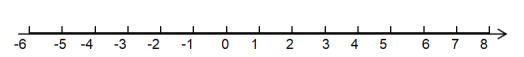
(2)小明家距小林家______千米
(3)若外卖小哥在骑车过程中每千米耗时3分钟,那么外卖小哥在整个过程中共用时多久?(假设外卖小哥一直在匀速行驶,在每户人家上门送外卖的时间忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
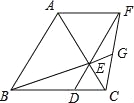
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com