
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,
, ![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,给出四个结论:①
,给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论有 ( )
;其中正确的结论有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题解析:如图,

过E作EQ⊥AB于Q,
∵∠ACB=90°,AE平分∠CAB,
∴CE=EQ,
∵∠ACB=90°,AC=BC,
∴∠CBA=∠CAB=45°,
∵EQ⊥AB,
∴∠EQA=∠EQB=90°,
由勾股定理得:AC=AQ,
∴∠QEB=45°=∠CBA,
∴EQ=BQ,
∴AB=AQ+BQ=AC+CE,
∴③正确;
作∠ACN=∠BCD,交AD于N,
∵∠CAD=![]() ∠CAB=22.5°=∠BAD,
∠CAB=22.5°=∠BAD,
∴∠ABD=90°-22.5°=67.5°,
∴∠DBC=67.5°-45°=22.5°=∠CAD,
∴∠DBC=∠CAD,
在△ACN和△BCD中,
 ,
,
∴△ACN≌△BCD,
∴CN=CD,AN=BD,
∵∠ACN+∠NCE=90°,
∴∠NCB+∠BCD=90°,
∴∠CND=∠CDA=45°,
∴∠ACN=45°-22.5°=22.5°=∠CAN,
∴AN=CN,
∴∠NCE=∠AEC=67.5°,
∴CN=NE,
∴CD=AN=EN=![]() AE,
AE,
∵AN=BD,
∴BD=![]() AE,
AE,
∴①正确,②正确;
过D作DH⊥AB于H,
∵∠FCD=∠CAD+∠CDA=67.5°,
∠DBA=90°-∠DAB=67.5°,
∴∠FCD=∠DBA,
∵AE平分∠CAB,DF⊥AC,DH⊥AB,
∴DF=DH,
在△DCF和△DBH中
 ,
,
∴△DCF≌△DBH,
∴BH=CF,
由勾股定理得:AF=AH,
∴![]() ,
,
∴AC+AB=2AF,
AC+AB=2AC+2CF,
AB-AC=2CF,
∵AC=CB,
∴AB-CB=2CF,
∴④正确.
故选D


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 在同一平面内,过一点有且只有一条直线与已知直线垂直
B. 对顶角相等
C. 两直线平行,同位角相等
D. 同旁内角互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日,北京市的最低气温是-11℃,嘉兴市的最低气温是-1℃,则这一天北京的最低气温比嘉兴的最低气温低( )
A.-12℃
B.-10℃
C.10℃
D.12℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是边
是边![]() 上一动点(不与点
上一动点(不与点![]() 重合),以
重合),以![]() 为边在
为边在![]() 的下方作等边三角形
的下方作等边三角形![]() ,连接
,连接![]() .
.
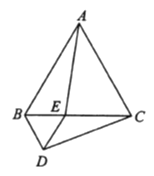
(1)在运动的过程中, ![]() 与
与![]() 有何数量关系?请说明理由.
有何数量关系?请说明理由.
(2)当![]() 时,求
时,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com