
(2009•武汉模拟)如图,O是△ABC的外接圆的圆心,∠ABC=60°,BF,CE分别是AC,AB边上的高且交于点H,CE交⊙O于M,D,G分别在边BC,AB上,且BD=BH,BG=BO,下列结论:①∠ABO=∠HBC;②AB•BC=2BF•BH;③BM=BD;④△GBD为等边三角形,其中正确结论的序号是( )

A.①② B.①③④ C.①②④ D.①②③④
D
【解析】
试题分析:①,延长AO交圆于点N,连接BN,可证明∠ABO=∠HBC.因此①正确;
②原式可写成 =
= ,无法直接用相似来求出,那么可通过相等的比例关系式来进行转换,不难发现三角形BEC中,∠ABC=60°,那么BC和BE存在倍数关系,即BC=2BE,因此如果证得
,无法直接用相似来求出,那么可通过相等的比例关系式来进行转换,不难发现三角形BEC中,∠ABC=60°,那么BC和BE存在倍数关系,即BC=2BE,因此如果证得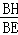 =
= ,可发现这个比例关系式正好是相似三角形BEH和BAF的两组对应线段,因此本题的结论也是正确的.
,可发现这个比例关系式正好是相似三角形BEH和BAF的两组对应线段,因此本题的结论也是正确的.
③要证MB=BD,先看与BD相等的线段有哪些,不难通过相似三角形ABN和BFC(一组直角,∠OBA=∠OAB=∠FBC)得出 ,将这个结论和②的结论进行置换即可得出:BD=BO=BH=BG,因此可证MB和圆的半径相等即可得出BM=BD的结论.如果连接NC,在三角形ANC中∠ANC=∠ABC=60°,因此AN=2NC,NC就是半径的长.通过相似三角形BME和CAE可得出
,将这个结论和②的结论进行置换即可得出:BD=BO=BH=BG,因此可证MB和圆的半径相等即可得出BM=BD的结论.如果连接NC,在三角形ANC中∠ANC=∠ABC=60°,因此AN=2NC,NC就是半径的长.通过相似三角形BME和CAE可得出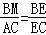 ,而在直角三角形BEC中,BE:EC=tan30°,而在直角三角形ANC中,NC:AC=tan30°,因此
,而在直角三角形BEC中,BE:EC=tan30°,而在直角三角形ANC中,NC:AC=tan30°,因此 ,即可得出BM=NC=BO=BD.因此该结论也成立.
,即可得出BM=NC=BO=BD.因此该结论也成立.
④在③中已经得出了BD=BG=BO=BH,而∠ABC=60°,因此三角形BGD是等边三角形.本结论也成立.
因此四个结论都成立,
【解析】
①延长AO交圆于点N,连接BN,则∠ABN=90°,又∠ACB=∠BNA,∠ABO=∠BAO,所以∠ABO=∠HBC.因此①正确;
②原式可写成 =
= ,∠ABC=60°,那么BC=2BE,因此
,∠ABC=60°,那么BC=2BE,因此 =
= ,所以本题的结论也是正确的.
,所以本题的结论也是正确的.
③∵△ABN∽△BFC(一组直角,∠OBA=∠OAB=∠FBC)∴ ,BD=BO=BH=BG,BM=BD.
,BD=BO=BH=BG,BM=BD.
连接NC,在三角形ANC中∠ANC=∠ABC=60°,∴AN=2NC,BE:EC=tan30°,
在直角三角形ANC中,NC:AC=tan30°, ,∴BM=NC=BO=BD.
,∴BM=NC=BO=BD.
因此该结论也成立.
④在③中已经得出了BD=BG=BO=BH,而∠ABC=60°,因此三角形BGD是等边三角形.本结论也成立.
因此四个结论都成立,
故选D.



科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上3.2圆的轴对称性1(解析版) 题型:?????
“两龙”高速公路是目前我省高速公路隧道和桥梁最多的路段.如图,是一个单心圆曲隧道的截面,若路面AB宽为10米,净高CD为7米,则此隧道单心圆的半径OA是( )
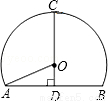
A.5 B.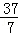 C.
C.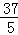 D.7
D.7
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上3.1圆1(解析版) 题型:?????
如图,以Rt△ABC的顶点A为圆心,斜边AB的长为半径作⊙A,则点C与⊙A的位置关系是( )
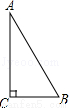
A.点C在⊙A内 B.点C在⊙A上 C.点C在⊙A外 D.不能确定
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上3.1圆1(解析版) 题型:?????
已知⊙O的半径为5,点P在⊙O内,则OP的长度可能为( )
A.3 B.5 C.7 D.8
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)九年级上1.3二次函数的性质2(解析版) 题型:解答题
根据条件求下列抛物线的解析式:
(1)二次函数的图象经过(0,1),(2,1)和(3,4);
(2)抛物线的顶点坐标是(﹣2,1),且经过点(1,﹣2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com