
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )
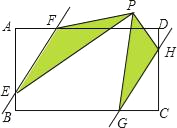
A. 7 B. 8 C. 12 D. 14
【答案】A
【解析】连接EG,FH,
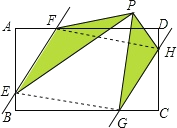
∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1,
∴AE=ABBE=41=3,
CH=CDDH=41=3,
∴AE=CH,
在△AEF与△CGH中,
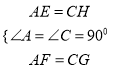 ,
,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得,△BGE≌△DFH,
∴EG=FH,
∴四边形EGHF是平行四边形,
∵△PEF和△PGH的高的和等于点H到直线EF的距离,
∴△PEF和△PGH的面积和=![]() ×平行四边形EGHF的面积,
×平行四边形EGHF的面积,
平行四边形EGHF的面积=4×6![]() ×2×3
×2×3![]() ×1×(62)
×1×(62) ![]() ×2×3
×2×3![]() ×1×(62) =243232,=14,
×1×(62) =243232,=14,
∴△PEF和△PGH的面积和=![]() ×14=7.
×14=7.
故选:A.


科目:初中数学 来源: 题型:
【题目】直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF//AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(_____,______),B(______,_____);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?
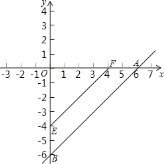
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过点B作PC的垂线,垂足为点H,连接HD、HQ. (14分)
(1)图中有________对相似三角形;
(2)若正方形ABCD的边长为1,P为AB的三等分点,求△BHQ的面积;
(3)求证:DH⊥HQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(π﹣3)0﹣(![]() )﹣2+(﹣1)2n
)﹣2+(﹣1)2n
(2)(m2)n(mn)3÷mn﹣2
(3)x(x2﹣x﹣1)
(4)(﹣3a)2a4+(﹣2a2)3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.

(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产![]() 两种设备,已知每台
两种设备,已知每台![]() 种设备的成本是
种设备的成本是![]() 种设备的1.5倍,公司若投入6万元生产
种设备的1.5倍,公司若投入6万元生产![]() 种设备,投人15万元生产
种设备,投人15万元生产![]() 种设备,则可生产两种设备共40台.请解答下列问题:
种设备,则可生产两种设备共40台.请解答下列问题:
(1)![]() 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?
(2)若![]() 两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中
两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中![]() 种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
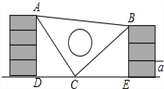
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com