
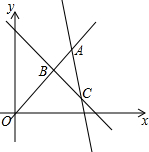
 已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积.
已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积. 分析 分别求出图中点A、B、C、E、F、G的坐标,根据三角形面积公式求出△ABC的面积.
解答 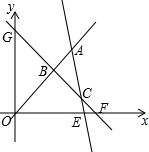 解:y1=x与y2=-3x+16的交点A的坐标为(4,4),
解:y1=x与y2=-3x+16的交点A的坐标为(4,4),
y2=-3x+16与y3=-x+6的交点C的坐标为(5,1),
y1=x与y3=-x+6的交点B的坐标为(3,3),
y3=-x+6与x轴的交点F的坐标为(6,0),与y轴的交点G的坐标为(0,6),
y2=-3x+16与x轴的交点E的坐标为($\frac{16}{3}$,0),
则△AOE的面积:$\frac{1}{2}$×$\frac{16}{3}$×4=$\frac{32}{3}$,
四边形OECB的面积:$\frac{1}{2}$×6×6-$\frac{1}{2}$×6×3-$\frac{1}{2}$×$\frac{2}{3}$×1=$\frac{26}{3}$,
则△ABC的面积=△AOE的面积-四边形OECB的面积=2.
点评 本题考查的是两条直线的交点的求法以及直线与坐标轴的交点的求法,正确解出二元一次方程组得到两条直线的交点是解题的关键,注意坐标与图形的关系.


科目:初中数学 来源: 题型:解答题
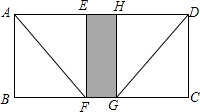 如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm
如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=$\frac{3}{5}$,AB=4.
如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=$\frac{3}{5}$,AB=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,F是AD边上一点,延长BF、CD交于点E.
如图,平行四边形ABCD中,F是AD边上一点,延长BF、CD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则该平行四边形ABCD的面积为12.
在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则该平行四边形ABCD的面积为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com