
已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2),
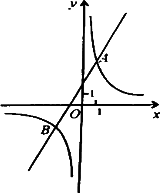
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
|
分析:(1)先根据点A的坐标求出反比例函数的解析式为y1=- (2)在一次函数的解析式中,令x=0,得出对应的y2的值,即得出直线y2=-x-1与y轴交点C的坐标,从而求出△AOC的面积; (3)当一次函数的值小于反比例函数的值时,直线在双曲线的下方,直接根据图象写出一次函数的值小于反比例函数的值x的取值范围-2<x<0或x>1. 解答:解:(1)∵函数y1= ∴m=-2,即y1=- 又∵点B(a,-2)在y1=- ∴a=1,∴B(1,-2).(3分) 又∵一次函数y2=kx+b过A、B两点, 即 解之得 ∴y2=-x-1.(5分) (2)∵x=0,∴y2=-x-1=-1, 即y2=-x-1与y轴交点C(0,-1).(6分) 设点A的横坐标为xA, ∴△AOC的面积S△OAC= (3)要使y1>y2,即函数y1的图象总在函数y2的图象上方.(8分) ∴-2<x<0,或x>1.(10分) 点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式.以及三角形面积的求法,这里体现了数形结合的思想. |
|
反比例函数与一次函数的交点问题. |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:北京市四中2011-2012学年八年级下学期期中考试数学试题 题型:044
已知反比例函数y1=![]() (k<0)的图象过点A(-
(k<0)的图象过点A(-![]() ,m),过点A作AB⊥x轴于点B,且△AOB的面积为
,m),过点A作AB⊥x轴于点B,且△AOB的面积为![]() .
.

(1)求k和m的值;
(2)若一次函数y2=ax+1的图象经过点A,并且与x轴相交于点C,求AO∶AC的值;
查看答案和解析>>
科目:初中数学 来源:重庆市巴南区全善学校2010届初三第三次月考数学试题 题型:044
已知反比例函数y1=![]() 与一次函数y2=mx+n的图象交与A、B两点,过点A作AD⊥x轴于点D,直线y2=mx+n经过线段OD的中点C,且△ADC的面积是2.若点A的横坐标是-4.
与一次函数y2=mx+n的图象交与A、B两点,过点A作AD⊥x轴于点D,直线y2=mx+n经过线段OD的中点C,且△ADC的面积是2.若点A的横坐标是-4.

(1)求反比例函数和一次函数的解析式;
(2)根据图象,直接写出x为何值时,y1>y2
查看答案和解析>>
科目:初中数学 来源:2006年湖南省常德市初中毕业生学业考试数学试卷 题型:044
如下图,已知反比例函数y1=![]() (m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.
(m≠0)的图象经过点A(-2,1),一次函数y2=kx+b(k≠0)的图象经过点C(0,3)与点A,且与反比例函数的图象相交于另一点B.
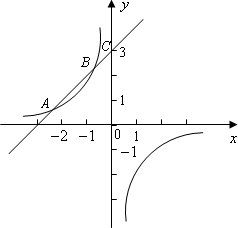
(1)分别求出反比例函数与一次函数的解析式;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源:2013年甘肃省兰州市高级中等学校招生考试数学A卷 题型:044
已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
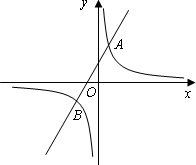
(1)求这两个函数的表达式;
(2)观察图象,当x>0时,直接写出y1>y2时自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com