
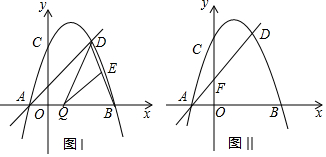
分析 (1)待定系数法得到抛物线的解析式为:y=-$\frac{1}{2}$x2+x+4;直线AD的解析式为y=x+2;
(2)如图1,作EG⊥x轴,设Q(m,0),根据相似三角形的性质得到EG=$\frac{8-2m}{3}$,求得S△QDE=S△BDQ-S△BEQ=$\frac{1}{2}$×(4-m)×4-$\frac{1}{2}×$(4-m)×$\frac{8-2m}{3}$=-$\frac{1}{3}$m2+$\frac{2}{3}$m+$\frac{8}{3}$=-$\frac{1}{3}$(m-1)2+3,根据二次函数的性质即可得到结论;
(3)①如图2,若CF为平行四边形的一边,则点N于抛物线的顶点重合,于是得到点M的坐标(1,$\frac{5}{2}$),(1,$\frac{13}{2}$);②如图3,若CF为平行四边形的一条对角线,则CF与MN互相平分,过点M,N分别向x轴作垂线,垂足分别为H,K,MN与HK交于点P,即可得到结论.
解答  解:(1)根据题意得,$\left\{\begin{array}{l}{16a+4b+4=0}\\{-\frac{b}{2a}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
解:(1)根据题意得,$\left\{\begin{array}{l}{16a+4b+4=0}\\{-\frac{b}{2a}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{1}{2}$x2+x+4;
∵B(4,0),对称轴为x=1,
∴A(-2,0),
∵D(2,m)在抛物线的解析式y=-$\frac{1}{2}$x2+x+4上,
∴D(2,4),
设直线AD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-2k+b=0}\\{2k+b=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴直线AD的解析式为y=x+2;
(2)如图1,作EG⊥x轴,设Q(m,0),
∵QE∥AD,
∴△BEQ∽△BDA,
∴$\frac{BQ}{BA}=\frac{EG}{4}$,
即$\frac{4-m}{6}=\frac{EG}{4}$,
解得:EG=$\frac{8-2m}{3}$,
∴S△BEQ=$\frac{1}{2}$×(4-m)×$\frac{8-2m}{3}$,
∴S△QDE=S△BDQ-S△BEQ=$\frac{1}{2}$×(4-m)×4-$\frac{1}{2}×$(4-m)×$\frac{8-2m}{3}$=-$\frac{1}{3}$m2+$\frac{2}{3}$m+$\frac{8}{3}$=-$\frac{1}{3}$(m-1)2+3,
∴△QED面积的最大值是3;
(3)∵直线AD交y轴于点F,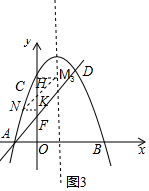
∴F(0,2),
∵抛物线的顶点坐标(1,$\frac{9}{2}$),
①如图2,若CF为平行四边形的一边,则点N于抛物线的顶点重合,此时,MN=CF=2,
∴点M的坐标(1,$\frac{5}{2}$),(1,$\frac{13}{2}$);
②如图3,若CF为平行四边形的一条对角线,则CF与MN互相平分,
过点M,N分别向x轴作垂线,垂足分别为H,K,MN与HK交于点P,
易得△MHP≌△NKP,
∴点M,N的横坐标分别是1,-1,
∴N(-1,$\frac{5}{2}$),
∴PK=$\frac{1}{2}$=HP,
∴HO=$\frac{7}{2}$,
∴M(1,$\frac{7}{2}$),
综上所述,点M的坐标为:(1,$\frac{5}{2}$)或(1,$\frac{13}{2}$)或(1,$\frac{7}{2}$).
点评 本题考查了待定系数法求函数的解析式,相似三角形的判定和性质,平行四边形的判定和性质,全等三角形的性质,正确的作出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
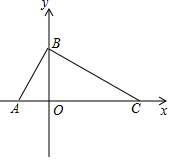 如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.
如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
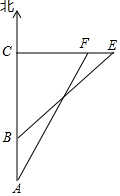 钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)
钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
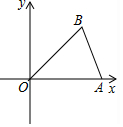 如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )
如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )| A. | 向左平移1个单位,再向下平移1个单位 | |
| B. | 向左平移(2$\sqrt{2}$-1)个单位,再向上平移1个单位 | |
| C. | 向右平移$\sqrt{2}$个单位,再向上平移1个单位 | |
| D. | 向右平移1个单位,再向上平移1个单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com