
【题目】暑假期间小王和小吴两家6个人一起外出旅游,乘坐两辆出租车前往飞机场,在离机场11千米处一辆车出了故障,不能行驶.此时离机场停止办理登机手续时间还有半个小时,唯一可以利用的交通工具只有一辆出租车,连同司机在内限乘5人,车速60千米/时.
(1)如果2人在原地等候,这辆车分两批接送,6人都能及时到达机场吗?
(2)如果在汽车送第一批人的同时,余下2人以6千米/时的速度向前步行,汽车在将第一批人送达后即返回接第二批人,他们能及时到达机场吗?
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
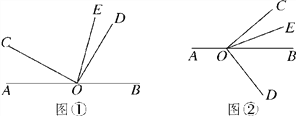
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=![]() ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含![]() 的代数式表示);
的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为AB上面半圆上一点,点D为AB的下面半圆的中点,连接CD与AB交于点E,延长BA至F,使EF=CF. 
(1)求证:CF与⊙O相切;
(2)若DEDC=13,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有下列四种结论:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC.以其中的2个结论作为依据不能判定△ABC≌△ADC的是( )
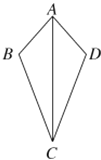
A. ①② B. ①③ C. ①④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若一个三位数的十位上数字为7,且从4、5、6、8中随机选取两数,与7组成“中高数”,那么组成“中高数”的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距70千米,甲从A地出发,每小时行15千米,乙从B地出发,每小时行20千米.
(1)若两人同时出发,相向而行,则经过几小时两人相遇?
(2)若甲在前,乙在后,两人同时同向而行,则几小时后乙追上甲?
(3)若两人同时出发,相向而行,则几小时后两人相距10千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读后解决问题:
在“15.3分式方程”一课的学习中,老师提出这样的一个问题:如果关于x的分式方程![]() 的解为正数,那么a的取值范围是什么?
的解为正数,那么a的取值范围是什么?
经过交流后,形成下面两种不同的答案:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.
因为解是正数,可得a﹣2>0,所以a>2.
小强说:本题还要必须a≠3,所以a取值范围是a>2且a≠3.
(1)小明与小强谁说的对,为什么?
(2)关于x的方程![]() 有整数解,求整数m的值.
有整数解,求整数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com