
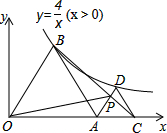
 如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=$\frac{4}{x}$(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积=4.
如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=$\frac{4}{x}$(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积=4. 分析 设等边△AOB的边长为a,根据等边三角形的性质可得出点B的坐标,由反比例函数图象上点的坐标特征即可得出$\frac{1}{2}$a•$\frac{\sqrt{3}}{2}$a=4,结合三角形的面积公式可得出S△OBA=$\frac{1}{2}$a•$\frac{\sqrt{3}}{2}$a=4,再根据等边三角形的性质可得出∠BOA=∠DAC=60°,由此得出OB∥AD,依照面积法即可得出S△OBP=S△OBA=4,此题得解.
解答 解:设等边△AOB的边长为a,则点B的坐标为($\frac{1}{2}$a,$\frac{\sqrt{3}}{2}$a),
∵点B在双曲线y=$\frac{4}{x}$(x>0)上,
∴$\frac{1}{2}$a•$\frac{\sqrt{3}}{2}$a=4,
∴S△OBA=$\frac{1}{2}$a•$\frac{\sqrt{3}}{2}$a=4.
∵△AOB与△ACD均为正三角形,
∴∠BOA=∠DAC=60°,
∴OB∥AD,
∴S△OBP=S△OBA=4.
点评 本题考查了等边三角形的性质、反比例函数图象上点的坐标特征、三角形的面积公式以及平行线的性质,解题的关键是用a表示出S△OBP.本题属于中档题,难度不大,解决该题型题目时,通过平行线的性质利用面积法找出面积相等的三角形是关键.


科目:初中数学 来源: 题型:选择题
| A. | 0.668×109 | B. | 6.68×10-9 | C. | 6.68×109 | D. | 66.8×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的直径垂直于弦 | |
| B. | 与直径垂直的直线是圆的切线 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 联结等腰梯形四边中点的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “任意画一个三角形,其内角和为360°”是随机事件 | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投十次可投中6次 | |
| C. | 抽样调查选取样本时,所选样本可按自己的喜好选取 | |
| D. | 检测某城市的空气质量,采用抽样调查法 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
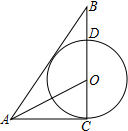 如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )
如图,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( )| A. | π | B. | 2π | C. | $\frac{9}{4}π$ | D. | $\frac{16}{9}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com