
分析 解方程组得到$\left\{\begin{array}{l}{a=\frac{40}{3}+\frac{2c}{3}}\\{b=\frac{95}{3}-\frac{5c}{3}}\end{array}\right.$,根据已知条件得到10≤c≤$\frac{125}{8}$,求得c为10,11,12,13,14,15,得到a的对应整数值为20,无整数值,无整数值,22,无整数值,无整数值,求出c=10或13;即可得到结论.
解答 解:$\left\{\begin{array}{l}{a+b+c=45}\\{600a+2400b+3600c=84000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{40}{3}+\frac{2c}{3}}\\{b=\frac{95}{3}-\frac{5c}{3}}\end{array}\right.$,
由|c-a|≤10,得|c-40|≤30,
解得10≤c≤70①,
由|b-c|≤10得|8c-95|≤30,
解得$\frac{65}{8}$≤c≤$\frac{125}{8}$②,
由①②得10≤c≤$\frac{125}{8}$,
∵c为正整数,
∴c为10,11,12,13,14,15,a的对应整数值为20,无整数值,无整数值,22,无整数值,无整数值,
∴c=10或13;
当c=10时,b=15,当c=13时,b=10,
∴它们的正整数解为:$\left\{\begin{array}{l}{a=20}\\{b=15}\\{c=10}\end{array}\right.$,或$\left\{\begin{array}{l}{a=22}\\{b=10}\\{c=13}\end{array}\right.$
点评 本题考查了三元一次方程组,解不等式,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,下列描述正确的是( )
如图,下列描述正确的是( )| A. | 射线OA的方向是北偏东方向 | B. | 射线OB的方向是北偏西65° | ||
| C. | 射线OC的方向是东南方向 | D. | 射线OD的方向是西偏南15° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
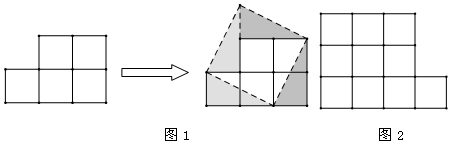
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
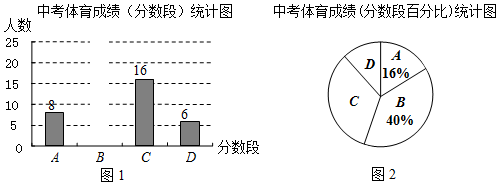
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 五子棋是一种两人对弈的棋类游戏,规则是:一方执黑子,一方执白子,由黑方先行,白方后行,在正方形棋盘中,双方交替下子,每次只能下一子,下在棋盘横线与竖线的交叉点上,最先在棋盘横向、竖向或斜向形成连续的相同颜色五个棋子的一方为胜,如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);此时轮到黑方下子,记其此步所下黑子为C,为了保证不让白方在两步之内(含两步)获胜,黑子C的坐标应该为(3,7)或(7,3).
五子棋是一种两人对弈的棋类游戏,规则是:一方执黑子,一方执白子,由黑方先行,白方后行,在正方形棋盘中,双方交替下子,每次只能下一子,下在棋盘横线与竖线的交叉点上,最先在棋盘横向、竖向或斜向形成连续的相同颜色五个棋子的一方为胜,如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);此时轮到黑方下子,记其此步所下黑子为C,为了保证不让白方在两步之内(含两步)获胜,黑子C的坐标应该为(3,7)或(7,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com