
 以△ABC的边BC为一边向三角形外侧作正方形BDEC,连结AD、AE分别交BC于点F、G,过点F、G分别作BC的垂线交AB、AC于点H、K,试判断四边形HFGK的形状.
以△ABC的边BC为一边向三角形外侧作正方形BDEC,连结AD、AE分别交BC于点F、G,过点F、G分别作BC的垂线交AB、AC于点H、K,试判断四边形HFGK的形状. 分析 由BD⊥BC,HF⊥BC,得到HF∥BD,根据平行线分线段成比例得到$\frac{AH}{AB}=\frac{AF}{AD}$,同理:$\frac{AK}{AC}=\frac{AG}{AE}$,根据BC∥DE,于是得到$\frac{AF}{AD}=\frac{AG}{AE}$,即$\frac{AH}{AB}=\frac{AK}{AC}$,证得四边形HFGK是矩形,由于$\frac{HF}{BD}=\frac{AH}{AB}$,$\frac{HK}{BC}=\frac{AH}{AB}$,于是得到$\frac{FH}{BD}=\frac{HK}{BC}$,求得HK=FH,即可得到结论.
解答 解:四边形HFGK是正方形,
理由:BD⊥BC,HF⊥BC,
∴HF∥BD,
∴$\frac{AH}{AB}=\frac{AF}{AD}$,
同理:$\frac{AK}{AC}=\frac{AG}{AE}$,
∵四边形BDEC是正方形,
∴BC∥DE,
∴$\frac{AF}{AD}=\frac{AG}{AE}$,
∴$\frac{AH}{AB}=\frac{AK}{AC}$,
∴HK∥BC,则HK∥FG,
又∵HF⊥BC,KG⊥BC,
∴HF∥KG,
∴四边形HFGK是矩形,
∵$\frac{HF}{BD}=\frac{AH}{AB}$,$\frac{HK}{BC}=\frac{AH}{AB}$,
∴$\frac{FH}{BD}=\frac{HK}{BC}$,
∵BD=BC,
∴HK=FH,
∴四边形HFGK是正方形.
点评 本题考查了相似三角形的判定和性质,正方形的判定和性质,熟练掌握各定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
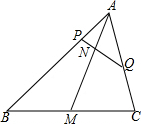 如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.9a元 | B. | 1.2a元 | C. | 1.26a元 | D. | 1.4a元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD、AD与BC之间有什么样的位置关系,说明理由.除前面的结论外.你还能得到哪些结论?请写出来.
在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD、AD与BC之间有什么样的位置关系,说明理由.除前面的结论外.你还能得到哪些结论?请写出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
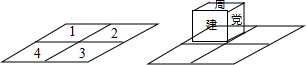 如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.
如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com