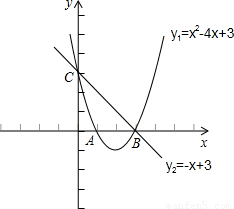
在平面直角坐标系xOy中,抛物线y1=x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B、C两点.
(1)求直线BC解析式y2及抛物线的解析式;
(2)求x满足什么条件时,y1<y2;
(3)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形求所有满足条件点P的坐标.
【答案】
分析:(1)依题意设直线BC的解析式为y=kx+3,把B点坐标代入解析式求出直线BC的表达式,然后又已知抛物线y=x
2+bx+c过点B,C,代入求出解析式.
(2)画出图象,找到y
1在y
2下面时,x的取值范围即可,也可联立y
1、y
2的解析式,运用不等式求解.
(3)分两种情况讨论,①当PQ∥AB时,此时根据PQ=AB=2,可得出点P的横坐标,代入即可得出点P的坐标;②②当P、Q为对角顶点时,作PD⊥x轴于D点,此时根据AD=OB可求出点P的横坐标为4,继而代入可得出点P的纵坐标.
解答:解:(1)由题意得:直线BC为y
2=kx+3,把B(3,0)代入得:3k+3=0,
解得:k=-1,
故直线BC的解析式为y=-x+3,
从而可得点C坐标为(0,3),
把B、C两点代入y
1=x
2+bx+c得

,
解得:

,
故抛物线的解析式为y
1=x
2-4x+3.
(2)由图可知:当0<x<3时,y
1<y
2.
(3)①当PQ∥AB时,

则PQ=AB=2,
从而可得点P的横坐标为2或-2,
当x=2时,y=-1;
当x=-2时,y=15,
故P
1为(2,-1),P
2为(-2,15),
②当P、Q为对角顶点时,作PD⊥x轴于D点,

则有OB=BQ×cos∠QBO,AD=APcos∠PAD,
∵四边形ABCD是平行四边形,
∴AP=BQ,∠QBO=∠PAD,
∴AD=OB=3,
则可得点P的横坐标为4,当x=4时,y=3,
所以P
3为(4,3).
综上可得符合题意的点P的坐标有三个:P
1(2,-1),P
2(-2,15),P
3(4,3).
点评:此题考查了二次函数的综合题,涉及了待定系数法求函数解析式、平行四边形的判定与性质,难点在第三问,需要分类讨论,不要漏解.

 ,
, ,
,




 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案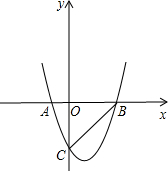 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为