
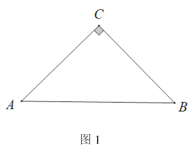
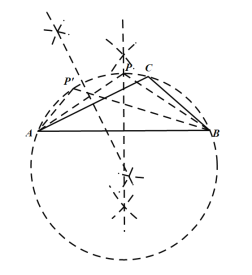
【题目】(1)如图1,△ABC 中,AC=BC,∠ACB=90°.请用直角三角尺(仅可画直角或直线)在图中画出一个点P,使得∠APB=45°;
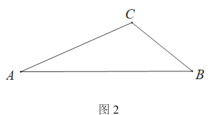
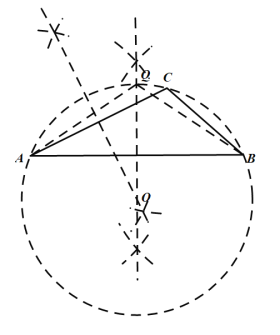
(2)如图2,△ABC 中,AB=a,∠ACB=![]() ,请用直尺和圆规作出一个点Q,使点Q与点C在AB同侧,QA=QB,∠AQB=
,请用直尺和圆规作出一个点Q,使点Q与点C在AB同侧,QA=QB,∠AQB=![]() ;(不写作法,保留作图痕迹)
;(不写作法,保留作图痕迹)
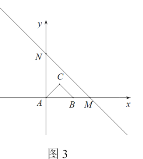
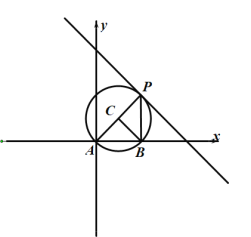
(3)如图3,若 AC=BC=![]() ,∠ACB=90°,以点A为原点,直线AB 为 x 轴,过点A垂直于AB的直线为 y 轴,建立平面直角坐标系,直线y= - x+b(b>0)交 x 轴于点M,交 y 轴于点N.当点P在直线MN上,且∠APB=45°,求点P的个数及对应的b的取值范围;
,∠ACB=90°,以点A为原点,直线AB 为 x 轴,过点A垂直于AB的直线为 y 轴,建立平面直角坐标系,直线y= - x+b(b>0)交 x 轴于点M,交 y 轴于点N.当点P在直线MN上,且∠APB=45°,求点P的个数及对应的b的取值范围;
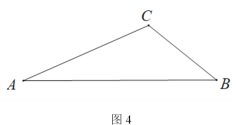
(4)如图4,△ABC 中,AB=a,∠ACB=![]() ,请用直尺和圆规作出点P,使得∠APB=
,请用直尺和圆规作出点P,使得∠APB=![]() 且AP+BP最大,请简要说明理由.(不写作法,保留作图痕迹)
且AP+BP最大,请简要说明理由.(不写作法,保留作图痕迹)
【答案】(1)见解析;(2)见解析;(3)当![]() 时,点P的个数为2个,当
时,点P的个数为2个,当![]() 或
或![]() 时,点P的个数为1个,当
时,点P的个数为1个,当![]() 时,点P有0个;(4)图见解析,理由见解析
时,点P有0个;(4)图见解析,理由见解析
【解析】
(1)画∠ABM=90°,延长AC与BM交于点P,则∠APB=45°;
(2)作△ACB的外接圆与AB的垂直平分线交于点Q,则AQ=BQ,∠AQB=∠ACB=![]() ;
;
(3)以点C为圆心,AC长为半径画圆,当直线![]() 恰好与圆相切时,此时处于临界点,求出此时b的值,然后通过对直线的平移即可确定b的取值范围,通过平移后直线与圆的交点的个数即可确定点P的个数;
恰好与圆相切时,此时处于临界点,求出此时b的值,然后通过对直线的平移即可确定b的取值范围,通过平移后直线与圆的交点的个数即可确定点P的个数;
(4)在问题(2)已作图像基础上,以点Q为圆心,AQ长为半径作圆,在![]() 上取一点
上取一点![]() 即可满足
即可满足![]() ,然后延长
,然后延长![]() 交⊙Q于点F,连接FB,易证
交⊙Q于点F,连接FB,易证![]() ,
,![]() ,当AF 为直径时最大,即点P为弧AB中点时最大.
,当AF 为直径时最大,即点P为弧AB中点时最大.
解:(1)如图:
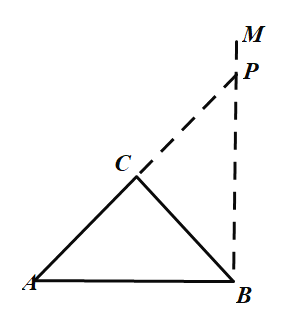
(2)如图:
(3)如图,以点C为圆心,AC长为半径画圆,当直线![]() 恰好与圆相切时,设切点为P,此时
恰好与圆相切时,设切点为P,此时![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴点P的坐标为![]() ,
,
将点P代入![]() 中得,
中得,![]()
解得![]() .
.
当直线恰好平移到与BC重合时,点B在直线上,将点B(2,0)代入![]() 中得,
中得,![]() ,解得
,解得![]() .
.
然后通过对直线![]() 的平移之后得到的新直线与圆的交点的个数即可得出P点的个数,
的平移之后得到的新直线与圆的交点的个数即可得出P点的个数,
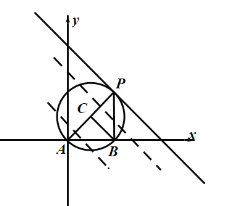
当![]() 时,不存在这样的P点,当
时,不存在这样的P点,当![]() 时,存在两个P点,当
时,存在两个P点,当![]() 时,虽然直线与圆有两个交点,但是其中一个点不满足题意,所以只存在一个P点.
时,虽然直线与圆有两个交点,但是其中一个点不满足题意,所以只存在一个P点.
综上所述,当![]() 时,点P的个数为2个,当
时,点P的个数为2个,当![]() 或
或![]() 时,点P的个数为1个,当
时,点P的个数为1个,当![]() 时,点P有0个,;
时,点P有0个,;
(4)如图,
理由如下:
在问题(2)已作图像基础上,以点Q为圆心,AQ长为半径作圆,在![]() 上取一点
上取一点![]() 即可满足
即可满足![]() ,然后延长
,然后延长![]() 交⊙Q于点F,连接FB,
交⊙Q于点F,连接FB,
![]()
![]() ,
,
![]()
![]()
![]()
当AF 为直径时最大,即点P为弧AB中点时最大



 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】 “宜居长沙”是我们的共同愿景,空气质量倍受人们的关注.我市某空气质量检测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:
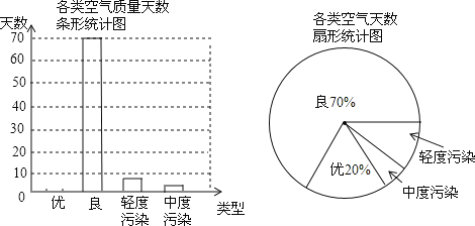
(1)统计图共统计了______天空气质量情况.
(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形圆心角度数.
(3)从小源所在班级的40名同学中,随机选取一名同学去该空气质量监测点参观,则恰好选到小源的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
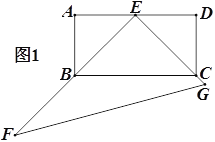
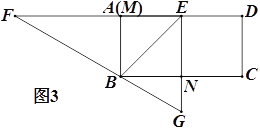
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
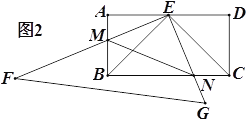
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.

(1)线段AB,BC,AC的长分别为AB= ,BC= ,AC= ;
(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.
请从下列A、B两题中任选一题作答,我选择 题.
A:①求线段AD的长;
②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.
B:①求线段DE的长;
②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠BAC=2∠EBC ,以AB为直径的⊙O交AC于点D,交EB于点F.
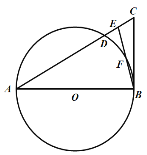
(1)求证:BC与⊙O相切;
(2)若AB=8,BE=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc>0;②b<a+c;③当x<0时,y随x的增大而增大;④2c<3b;⑤a+b>m(am+b)(其中m≠1)其中正确的个数是( )
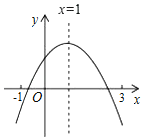
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)1978年,以中共十一届三中全会为标志,中国开启了改革开放历史征程.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.下图是1994—2017年三次产业对GDP的贡献率统计图(三次产业是指:第一产业是指农、林、牧、渔业(不含农、林、牧、渔服务业);第二产业是指采矿业(不含开采辅助活动),制造业(不含金属制品、机械和设备修理业),电力、热力、燃气及水生产和供应业,建筑业;第三产业即服务业,是指除第一产业、第二产业以外的其他行业).下列推断不合理的是( )
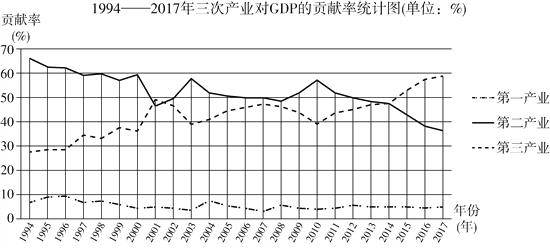
A. 2014年,第二、三产业对GDP的贡献率几乎持平;
B. 改革开放以来,整体而言三次产业对GDP的贡献率都经历了先上升后下降的过程;
C. 第三产业对GDP的贡献率增长速度最快的一年是2001年;
D. 2006年,第二产业对GDP的贡献率大约是第一产业对GDP的贡献率的10倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x=t与反比例函数y=![]() ,y=﹣
,y=﹣![]() 的图象交于点A,B,直线y=2t与反比例y=
的图象交于点A,B,直线y=2t与反比例y=![]() ,y=﹣
,y=﹣![]() 的图象交于点C,D,其中常数t,k均大于0.点P,Q分别是x轴、y轴上任意点,若S△PCD=S1,S△ABQ=S2.则下列结论正确的是( )
的图象交于点C,D,其中常数t,k均大于0.点P,Q分别是x轴、y轴上任意点,若S△PCD=S1,S△ABQ=S2.则下列结论正确的是( )
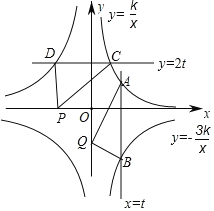
A.S1=2tB.S2=4kC.S1=2S2D.S1=S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com