

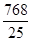 .(10分)
.(10分)

科目:初中数学 来源:不详 题型:单选题
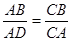 中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】
中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】 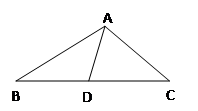
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
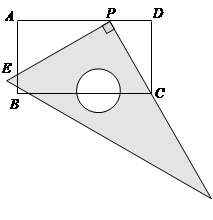 (3)是否存在这样的点P,使△CDP的周长等于△PAE周长的2倍?若存在,求DP的长;若不存在,请说明理由.
(3)是否存在这样的点P,使△CDP的周长等于△PAE周长的2倍?若存在,求DP的长;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
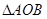 的顶点A、B在二次函数
的顶点A、B在二次函数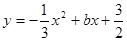 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在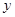 轴和
轴和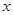 轴上,
轴上,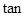 ∠ABO=
∠ABO=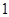 .
.
|
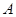 作
作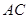 ∥
∥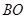 交上述函数图像于点
交上述函数图像于点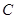 ,点
,点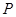 在上述函数图像上,当
在上述函数图像上,当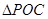 与
与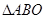 相似时,求点
相似时,求点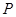 的坐标.(8分)
的坐标.(8分)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
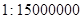 的卫星地图上,测得上海和南京的距离大约是
的卫星地图上,测得上海和南京的距离大约是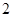 厘米.那么上海和南京的实际距离大约是 ▲ 千米.
厘米.那么上海和南京的实际距离大约是 ▲ 千米.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛
C=90°,以AB为直径的OM交OC于点D、E,连结AD、BD.现以O为坐标原点,OA、OC所在直线为x轴、y轴建立如图所示直角坐标系,若抛 物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
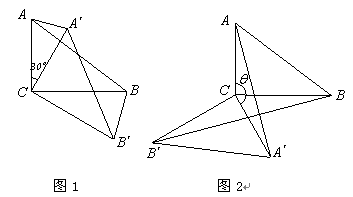
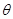 (0°<
(0°<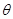 <180°)时,S△ACA′ 与S△BCB′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含
<180°)时,S△ACA′ 与S△BCB′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含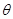 的代数式表示).
的代数式表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com