
【题目】在平面直角坐标系中,将直角三角形的直角顶点放在点![]() 处,两直角边与坐标轴交于如图所示的点
处,两直角边与坐标轴交于如图所示的点![]() 和点
和点![]() ,则
,则![]() 的值为______.
的值为______.

【答案】16
【解析】
过P作PM⊥x轴于M,PN⊥y轴于N,由P(8,8),得到PM=MO=ON=PN=8,由于∠MPB+∠BPN=∠MPN=90°,∠MPB+∠MPA=90°,于是得到∠BPN=∠MPA,推出△PBN≌△APM,根据全等三角形的性质得到AM=BN,然后根据线段的和差关系,即可得到结论;
解:如图,过P作PM⊥x轴于M,PN⊥y轴于N,
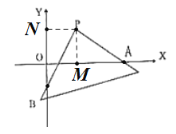
∵P(8,8),
∴PM=MO=ON=PN=8,
∵∠MPB+∠BPN=∠MPN=90°,∠MPB+∠MPA=∠APB=90°,
∴∠BPN=∠MPA,
∵∠BNP=∠AMP=90°,
∴△PBN≌△PAM(ASA),
∴BN=AM,
∴![]()
![]()
![]() ;
;
故答案为:16.


科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,A点表示2,现在点A向右移动两个单位后到达点B;再向左移动10个单位到达C点:
(1)请在数轴上表示出A点开始移动时位置及B、C点位置;
(2)当A点移动到C点时,若要再移动到原点,问必须向哪个方向移动多少个单位?
(3)请把A点从开始移动直至到达原点这一过程,用一个有理数算式表达出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
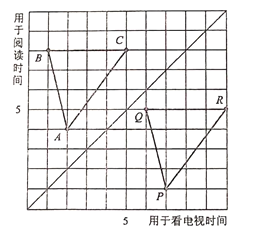
【题目】图中,点A,B,C,P,Q,R显示了6名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h)
(1)用有序数对表示图中点A,B,C,P,Q,R
(2)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(3)三角形ABC的图形经过怎样的变换后得到三角形PQR的图形?其中点A对应点P,点B对应点Q,点C对应点R
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204.
(1)写出商场卖这种服装每天的销售利润![]() 与每件的销售价
与每件的销售价![]() 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数![]() 的图像与性质进行了探究.请补充完整:
的图像与性质进行了探究.请补充完整:
(1)先填表,再在如图所示的平面直角坐标系中,描全表中各对对应值为坐标的点,并画出该函数的图像:
x | … | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | … |
| … | 2 |
| 3 | -3 |
| 0 | … |
(2)结合函数的图像,说出两条不同类型的性质;
①________________________________;____________________________________.
②![]() 的图像是由
的图像是由![]() 的图像如何平移得到?
的图像如何平移得到?
___________________________________________.
(3)当函数值![]() 时,x的取值范围是____________span>.
时,x的取值范围是____________span>.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,F是CD边上一点(不与C、D重合),过点D作DG⊥BF交BF延长线于点G.连接AG,交BD于点E,交CD于点M,连接EF.若DG=4,AG=![]() ,则EF的长为____________.
,则EF的长为____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com