
【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE. 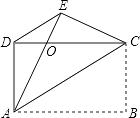
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,
又∵AC是折痕,
∴BC=CE=AD,
AB=AE=CD,
在△ADE与△CED中,
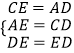 ,
,
∴△ADE≌△CED(SSS)
(2)证明:∵△ADE≌△CED,
∴∠EDC=∠DEA,
又∵△ACE与△ACB关于AC所在直线对称,
∴∠OAC=∠CAB,
∵∠OCA=∠CAB,
∴∠OAC=∠OCA,
∴2∠OAC=2∠DEA,
∴∠OAC=∠DEA,
∴DE∥AC
【解析】(1)根据矩形的性质和折叠的性质可得BC=CE=AD,AB=AE=CD,根据SSS可证△ADE≌△CED(SSS);(2)根据全等三角形的性质可得∠EDC=∠DEA,由于△ACE与△ACB关于AC所在直线对称,可得∠OAC=∠CAB,根据等量代换可得∠OAC=∠DEA,再根据平行线的判定即可求解.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
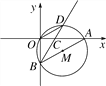
【题目】如图,在直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,-
,0)与点B(0,-![]() ),点D在劣弧
),点D在劣弧![]() 上,连结BD交x轴于点C,且∠COD=∠CBO.
上,连结BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A的坐标为A(0,a),将点A向右平移b个单位得到点B,其中a,b满足:(3a﹣2b)2+|a+b﹣5|=0. 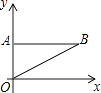
(1)求点B的坐标并求△AOB的面积S△AOB;
(2)在x轴上是否存在一点D,使得S△AOB=2S△AOD?若存在,求出D点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.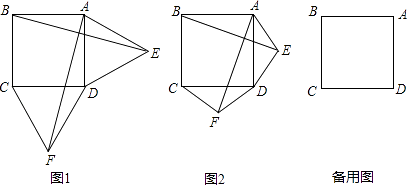
(1)请判断:AF与BE的数量关系是 , 位置关系是;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予说明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )
A.矩形
B.菱形
C.对角线相等的四边形
D.对角线互相垂直的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,-
,0)与点B(0,-![]() ),点D在劣弧
),点D在劣弧![]() 上,连结BD交x轴于点C,且∠COD=∠CBO.
上,连结BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果x=3m+1,y=2+9m,那么用x的代数式表示y为( )
A. y=2x B. y=x2 C. y=(x﹣1)2+2 D. y=x2+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com