练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

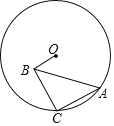
    【题目】如图，已知A、C是半径为2的⊙O上的两动点，以AC为直角边在⊙O内作等腰Rt△ABC，∠C=90°．连接OB．则OB的最小值为_____．

    【答案】

    【解析】

    如图，作等腰直角三角形△OCO′，CO=CO′，∠OCO′=90°，首先证明当点C固定时，点B在以O′为圆心OA为半径的圆上运动，推出当O、B、O′共线时，OB的值最小，最小值=OO′-O′B=2-2．

    解：如图，作等腰直角三角形△OCO′，CO=CO′，∠OCO′=90°，

    ∵AC=CB，∠ACB=∠OCO′，

    ∴△ACO≌△BCO′，

    ∴OA=O′B，

    ∴当点C固定时，点B在以O′为圆心OA为半径的圆上运动，

    ∴当O、B、O′共线时，OB的值最小，最小值=OO′-O′B=2-2．

    故答案为2-2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某城市为了加强公民的节气和用气意识，按以下规定收取每月煤气费：所用煤气如果不超过50立方米，按每立方米0.8元收费；如果超过50立方米，超过部分按每立方米1.2元收费设小丽家每月所用煤气量为x立方米，应交煤气费为y元.

    （1）若小丽家某月所用煤气量为80立方米，则小丽家该月应交煤气费多少元？

    （2）试写出y与x之间的解析式.

    （3）若小丽家4月份的煤气费为88元，则她家4月份所用煤气量为多少立方米？

    （4）已知小丽家6月份所交的煤气费平均每立方米为0.95元，那么6月份小丽家用了多少立方米的煤气？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中秋节期间某水库养殖场为适应市场需求，连续用天时间，采用每天降低水位以减少捕捞成本的办法．对水库中某种鲜鱼进行捕捞销售，第天（且为整数）的捕捞与销售的相关信息如下：

    鲜鱼销售单价（元）

    单位捕捞成本（元）

    捕捞量

    假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出．

    （1）求第天的收入（元）与（天）之间的函数关系式？（当天收入日销售额-日捕捞成本）

    （2）在第几天取得最大值，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正方形ABCD的对角线AC，BD相交于点O．

    （1）如图1，E，G分别是OB，OC上的点，CE与DG的延长线相交于点F．若DF⊥CE，求证：OE=OG；

    （2）如图2，H是BC上的点，过点H作EH⊥BC，交线段OB于点E，连结DH交CE于点F，交OC于点G．若OE=OG，

    ①求证：∠ODG=∠OCE；

    ②当AB=1时，求HC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

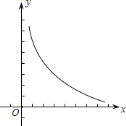
    【题目】已知图中的曲线是反比例函数（为常数）图象的一支．

    这个反比例函数图象的另一支在第几象限？常数的取值范围是什么？

    若该函数的图象与正比例函数的图象在第一象内限的交点为，过点作轴的垂线，垂足为，当的面积为时，求点的坐标及反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DCB中，AC与BD相交于点O，下列四组条件中，不能证明△ABC≌△DCB的是（　　）

    A.AB＝DC，AC＝DBB.AB＝DC，∠ABC＝∠DCB

    C.BO＝CO，∠A＝∠DD.∠ABD＝∠DCA，∠A＝∠D

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某大型水果超市销售无锡水蜜桃，根据前段时间的销售经验，每天的售价x（元/箱）与销售量y（箱）有如表关系：

    每箱售价x（元）

    68

    67

    66

    65

    …

    40

    每天销量y（箱）

    40

    45

    50

    55

    …

    180

    已知y与x之间的函数关系是一次函数．

    （1）求y与x的函数解析式；

    （2）水蜜桃的进价是40元/箱，若该超市每天销售水蜜桃盈利1600元，要使顾客获得实惠，每箱售价是多少元？

    （3）七月份连续阴雨，销售量减少，超市决定采取降价销售，所以从7月17号开始水蜜桃销售价格在（2）的条件下，下降了m%，同时水蜜桃的进货成本下降了10%，销售量也因此比原来每天获得1600元盈利时上涨了2m%（m＜100），7月份（按31天计算）降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】己知：二次函数y=ax2+bx+6（a≠0）与x轴交于A，B两点（点A在点B的左侧），点A，点B的横坐标是一元二次方程x2﹣4x﹣12=0的两个根．

    （1）求出点A，点B的坐标．

    （2）求出该二次函数的解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

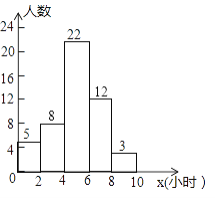
    【题目】某校为了解全校1600名学生每周课外体育活动时间的情况，随机调查了其中的部分学生，对这些学生每周课外体育活动时间x（单位：小时）进行了统计，根据所得数据绘制了一幅统计图，根据以上信息及统计图解答下列问题

    （1）本次接受随机抽样调查的学生人数为______；

    （2）求这些学生每周课外体育活动时间的平均数________；

    （3）估计全校学生每周课外体育活动时间不少于4小时的人数________．

    查看答案和解析>>

    同步练习册答案