
【题目】矩形ABCD中,AB=8,AD=6,E为BC边上一点,将△ABE沿着AE翻折,点B落在点F处,当△EFC为直角三角形时BE=_____.
【答案】3或6
【解析】
分当点F落在矩形内部时和当点F落在AD边上时两种情况求BE得长即可.
当△CEF为直角三角形时,有两种情况:

当点F落在矩形内部时,如图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=![]()
![]() =10,
=10,
∵∠B沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
当△CEF为直角三角形时,只能得到∠EFC=90°,
∴点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,如图,
∴EB=EF,AB=AF=6,
∴CF=10﹣6=4,
设BE=x,则EF=x,CE=8﹣x,
在Rt△CEF中,
∵EF2+CF2=CE2,
∴x2+42=(8﹣x)2,
解得x=3,
∴BE=3;
②当点F落在AD边上时,如图2所示.
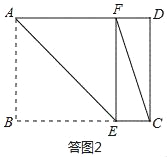
此时ABEF为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故答案为:3或6.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D、E分别在BC、AC上,且CD=AE,AD与BE相交于P,BQ⊥AD于Q.
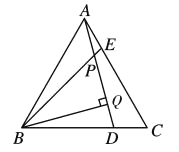
(1)求证:![]() ;
;
(2)若PQ=4,PE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE
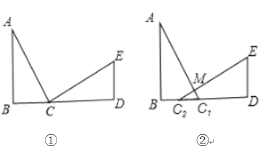
(1)求证:△ABC≌△CDE
(2)试判断AC与CE的位置关系,并说明理由.
(3)若将CD沿CB方向平移得到图②的情形,其余条件不变,此时第(2)问中AC与CE的位置关系还成立吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,
(1)求证:M是BE的中点.
(2)若CD=1,DE=![]() ,求△ABD的周长.
,求△ABD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.

(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
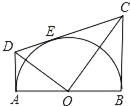
【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,对于下列结论:
①OD2=DECD;②AD+BC=CD;③OD=OC;④S梯形ABCD=![]() CDOA;⑤∠DOC=90°,
CDOA;⑤∠DOC=90°,
其中正确的是_____.(只需填上正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为8,AD是BC边上的中线,点E是AC边上的一点,AE=2,若点M是线段AD上的一个动点,则ME+MC的最小值为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行20分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是___________海里.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com