
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����T��һ��P�������������ߣ��е�ֱ�ΪM��N����![]() �����PΪ��T�Ļ��Ƶ㣮
�����PΪ��T�Ļ��Ƶ㣮

(1)����O�뾶Ϊ1ʱ��
����![]() �У���O�Ļ��Ƶ���_________;
�У���O�Ļ��Ƶ���_________;
��ֱ��y=2x+b��x�ύ�ڵ�A��y�ύ�ڵ�B�����߶�AB�ϴ��ڡ�O�Ļ��Ƶ㣬��b��ȡֵ��Χ��
(2)��T�İ뾶Ϊ1��Բ��Ϊ��0��t������![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶������Բ����ͼ��H������ͼ��H�ϴ��ڡ�T�Ļ��Ƶ㣬ֱ��д��t��ȡֵ��Χ.
Ϊ�뾶������Բ����ͼ��H������ͼ��H�ϴ��ڡ�T�Ļ��Ƶ㣬ֱ��д��t��ȡֵ��Χ.
���𰸡���1����![]() ����b��ȡֵ��ΧΪ
����b��ȡֵ��ΧΪ![]() ��
��![]() ����2��
����2��![]()
��������
��1�����ɻ��Ƶ㶨�弴�ɵó��𰸣�
�ڰ뾶Ϊ1�ġ�O�����л��Ƶ�����OΪԲ�ģ��뾶�ֱ�Ϊ1��2������Բ֮�䣨����ͼ��Ӱ������ʾ������Բ������СԲ��. ��������ۣ�����B��y����������ʱ����ͼ1��ͼ2��ʾ����ʱ����������������������߶�AB��뾶Ϊ2�ġ�O����ʱ��![]() ��
��
����B�����뾶Ϊ1�ġ�Oʱ��![]() .��Ϊ�߶�AB�ϴ��ڡ�O�Ļ��Ƶ㣬�ɻ��Ƶ㶨��ɵ�b��ȡֵ��Χ������B��y�Ḻ������ʱ����ͼ3��ͼ4��ʾ.Ҳ�ɵ�b��ȡֵ��Χ;
.��Ϊ�߶�AB�ϴ��ڡ�O�Ļ��Ƶ㣬�ɻ��Ƶ㶨��ɵ�b��ȡֵ��Χ������B��y�Ḻ������ʱ����ͼ3��ͼ4��ʾ.Ҳ�ɵ�b��ȡֵ��Χ;
��2��![]() .
.
��1����![]()
�ڰ뾶Ϊ1�ġ�O�����л��Ƶ�����OΪԲ�ģ��뾶�ֱ�Ϊ1��2������Բ֮�䣨����ͼ��Ӱ������ʾ������Բ������СԲ��.
��)����B��y����������ʱ����ͼ1��ͼ2��ʾ.
����������������������߶�AB��뾶Ϊ2�ġ�O����ʱ��![]() ��
��
����B�����뾶Ϊ1�ġ�Oʱ��![]() .
.
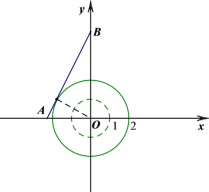

��Ϊ�߶�AB�ϴ��ڡ�O�Ļ��Ƶ㣬���Կɵ�b��ȡֵ��ΧΪ ![]() ��
��
�ڵ���B��y�Ḻ������ʱ����ͼ3��ͼ4��ʾ.
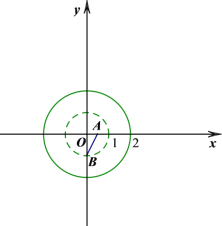

ͬ���ɵ�b��ȡֵ��ΧΪ ![]() .
.
���ϣ�b��ȡֵ��ΧΪ![]() ��
��![]()
��2��![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ���������У���ֱ�����5��Ԫ���У���֪2��Ԫ�أ�����������1���DZߣ����Ϳ�����������3��δ֪Ԫ��.�������������Σ�������Ҫ֪������Ԫ�ؾͿ�����������δ֪Ԫ���أ�˼��������������⣺
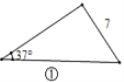
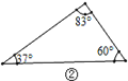

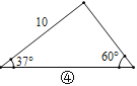

��1���۲�ͼ��~ͼ�ܣ�����ͼ�������ε���֪Ԫ�أ������������δ֪Ԫ�ص������____.
��2����ͼ�ݣ���![]() �У���֪
�У���֪![]() ��
��![]() ��
��![]() ���ܷ����BC�ij��ȣ�����ܣ������BC�ij��ȣ�������ܣ���˵������.���ο����ݣ�
���ܷ����BC�ij��ȣ�����ܣ������BC�ij��ȣ�������ܣ���˵������.���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
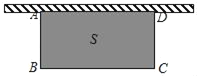
����Ŀ����ͼ������һ��ǽ��ǽ�ij��Ȳ��ޣ�����20m�����Χ��һ�����γ���ABCD���������ǽ��ֱ��һ��AB��xm�����ε����ΪSm2��
��1���ú�x��ʽ�ӱ�ʾS��
��2�������S��48m2����AB�ij���
��3����Χ��S��60m2�ľ�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У�AB��AD��BC��AD��EΪAB���е㣬��EC��ED�ֱ�Ϊ��BCD����ADC�Ľ�ƽ���ߣ�EF��CD��BC���ӳ����ڵ�G������DG.
��1����֤��CE��DE��
��2����AB=6����CF��DF��ֵ��
��3������BCE����DFG����ʱ��![]() ��ֵ�� .
��ֵ�� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ�ӹ���ڣ�ij�̵깺����һ���ɱ�Ϊÿ��30Ԫ�ļ�����Ʒ�������鷢�֣�����Ʒÿ���������![]() ����
����![]() �����۵���
�����۵���![]() ��Ԫ
��Ԫ![]() ����һ�κ�����ϵ����ͼ����ͼ��ʾ��
����һ�κ�����ϵ����ͼ����ͼ��ʾ��

��1�������Ʒÿ���������![]() �����۵���
�����۵���![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�����̵갴�����ڳɱ��ۣ��Ҳ�����60Ԫ�ĵ������ۣ������۵��۶�Ϊ���٣�����ʹ���۸���Ʒÿ���õ�����![]() ��Ԫ
��Ԫ![]() �����������Ƕ��٣�
�����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ��װ�����ɸ���ȫ��ͬ��A��B��C����������A��x����B��x����C��x+1��������������������һ������A��ĸ���Ϊ0.25��
��1���������A��B��C����������ٸ���
��2����С���ӿڴ������ģ��1����Żأ����������1���������û���״ͼ�ķ�����С������1��A���1��C��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3���˿��ƣ��ֱ��Ǻ���3������4�ͺ���5������ϴ�Ⱥ���ȳ�ȡһ�ţ����»�ɫ�����ֺ��ƷŻأ�ϴ�Ⱥ����ٳ�ȡһ�ţ�
��1���Ⱥ����γ�õ����ֱַ��Ϊx��y����������ͼ���б���|x��y|��1�ĸ��ʣ�
��2���ס�����������Ϸ���������ַ�����A�����������γ����ͬ��ɫ���ʤ��������ʤ��B�����������γ�����ֺ�Ϊ�������ʤ��������ʤ�����ʼ�ѡ�����ַ���ʤ�ʸ��ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������࣬���ҵ��չѸ�١�����ij��ݹ�˾������·���ʮ�·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ![]() �����
�����![]() ������ٶ��ù�˾ÿ�µ�Ͷ���ܼ�������������ͬ.
������ٶ��ù�˾ÿ�µ�Ͷ���ܼ�������������ͬ.
��1����ÿ�ݹ�˾ÿ�µ�Ͷ���ܼ�������ƽ�������ʣ�
��2��������˫ʮһ��������������Ԥ��11����Ͷ�ݵĿ���ܼ����������ʽ���ԭ��![]() �������ÿ��ÿ������Ͷ�ݿ��
�������ÿ��ÿ������Ͷ�ݿ��![]() ������ù�˾����
������ù�˾����![]() ��ҵ��Ա���Ƿ�����ɵ���Ͷ������������ܣ�����ʱ��Ƹ����ҵ��Ա��
��ҵ��Ա���Ƿ�����ɵ���Ͷ������������ܣ�����ʱ��Ƹ����ҵ��Ա��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��˫����y��![]() ��x��0��������OAB�Ķ���A��OB���е�C��AB��x�ᣬ��A������Ϊ��2��3����BE��x�ᣬ����ΪE��
��x��0��������OAB�Ķ���A��OB���е�C��AB��x�ᣬ��A������Ϊ��2��3����BE��x�ᣬ����ΪE��
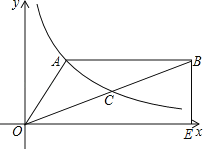
��1��ȷ��k��ֵ���� ����
��2��������OAB�������
��3������D��3��b����˫����y��![]() ��x��0���ϣ�ֱ��AD�Ľ���ʽΪy��mx+n����ֱ��д������ʽmx+n��
��x��0���ϣ�ֱ��AD�Ľ���ʽΪy��mx+n����ֱ��д������ʽmx+n��![]() �Ľ⼯���� ����
�Ľ⼯���� ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com