
分析 直线y=$\sqrt{3}$x+m经过点A(x1,0),可得x1=-$\frac{m}{\sqrt{3}}$,由x1是方程ax2+bx+c=0的根,也是方程$\sqrt{3}$x+m=0的根,推出x1是方程ax2+(b+$\sqrt{3}$)x+c+m=0的根,由关于x的方程ax2+(b+$\sqrt{3}$)x+c+m=0有两个相等的实数根,推出方程可以变形为a(x+$\frac{m}{\sqrt{3}}$)2=0,展开得到ax2+$\frac{2am}{\sqrt{3}}$x+$\frac{a{m}^{2}}{3}$=0,推出b=$\frac{2am}{\sqrt{3}}$-$\sqrt{3}$,c=$\frac{a{m}^{2}}{3}$-m,推出a(x1-x2)=±$\sqrt{{a}^{2}[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=±$\sqrt{{b}^{2}-4ac}$,代入计算即可.
解答 解:直线y=$\sqrt{3}$x+m经过点A(x1,0),
∴x1=-$\frac{m}{\sqrt{3}}$,
∵x1是方程ax2+bx+c=0的根,也是方程$\sqrt{3}$x+m=0的根,
∴x1是方程ax2+(b+$\sqrt{3}$)x+c+m=0的根,
∵关于x的方程ax2+(b+$\sqrt{3}$)x+c+m=0有两个相等的实数根,
∴方程可以变形为a(x+$\frac{m}{\sqrt{3}}$)2=0,展开得到ax2+$\frac{2am}{\sqrt{3}}$x+$\frac{a{m}^{2}}{3}$=0,
∴b=$\frac{2am}{\sqrt{3}}$-$\sqrt{3}$,c=$\frac{a{m}^{2}}{3}$-m,
∵a(x1-x2)=±$\sqrt{{a}^{2}[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=±$\sqrt{{b}^{2}-4ac}$=±$\sqrt{(\frac{2am}{\sqrt{3}}-\sqrt{3})^{2}-4a•(\frac{a{m}^{2}}{3}-m)}$=±$\sqrt{3}$,
故答案为±$\sqrt{3}$.
点评 本题考查抛物线与x轴的交点坐标、根的判别式、一次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考填空题中的压轴题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:填空题
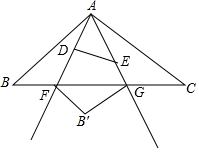 如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.
如图,在△ABC中,AB=AC=4,∠BAC=90°,以A为一个顶点的等腰Rt△ADE,∠ADE=90°,绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G,若点B关于直线AD的对称点为B′,当∠CFB′=60°时,则BF的长为$\frac{6\sqrt{2}-2\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
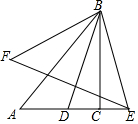 如图,在Rt△BAC中,∠ACB=Rt∠,AC=6,BC=8,D是AC边上的一点,点D关于BC的对称点为E,关于AB的对称点为F,连接BD,BE,BF,EF,若BD平分∠ABC,则EF的长为$\frac{16}{5}\sqrt{10}$.
如图,在Rt△BAC中,∠ACB=Rt∠,AC=6,BC=8,D是AC边上的一点,点D关于BC的对称点为E,关于AB的对称点为F,连接BD,BE,BF,EF,若BD平分∠ABC,则EF的长为$\frac{16}{5}\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
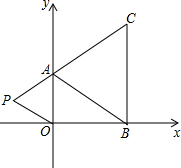 在如图直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系$\sqrt{a-2}+(b-3)^{2}$=0,(c-4)2≤0,点P、点A、点C在同一条直线上.
在如图直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系$\sqrt{a-2}+(b-3)^{2}$=0,(c-4)2≤0,点P、点A、点C在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
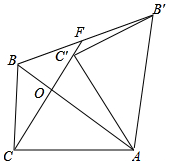 如图,在Rt△ABC中,∠ACB=90°,tan∠CBA=$\frac{4}{3}$,AB=5.将△ABC绕点A顺时针旋转得到△AB′C′,连接CC′并延长,交AB于点O,交BB′于点F.若CC′=CA,则BF=$\frac{5}{2}$.
如图,在Rt△ABC中,∠ACB=90°,tan∠CBA=$\frac{4}{3}$,AB=5.将△ABC绕点A顺时针旋转得到△AB′C′,连接CC′并延长,交AB于点O,交BB′于点F.若CC′=CA,则BF=$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
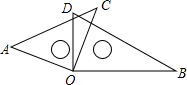 如图,将一副30°和45°的直角三角板的两个直角叠放在一起,使直角顶点重合于点O,若∠AOD=70°,则∠BOC的度数为( )
如图,将一副30°和45°的直角三角板的两个直角叠放在一起,使直角顶点重合于点O,若∠AOD=70°,则∠BOC的度数为( )| A. | 75° | B. | 70° | C. | 45° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com