
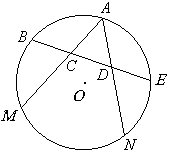
如图所示,M、N是⊙O上的两点,连接AM、NA,B、E是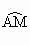 、
、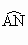 的中点,若
的中点,若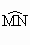 的度数为120°.求证:△ACD是正三角形.
的度数为120°.求证:△ACD是正三角形.
|
证明:连接 AB、AE.∵ B、E是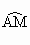 、 、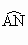 的中点,∴ 的中点,∴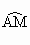 = =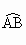 , ,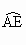 = = . .
∴∠ EAC=∠E,∠B=∠DAE.即∠B+∠BAC=∠E+∠DAE.∴∠ ACD=∠ADE.又 ∴△CAD是等边三角形. |
|
要证△ ACD是正三角形,由正三角形的判定方法可以直接证三边相等或先证是等腰三角形,再证有一个内角为60°.因∠CAD所对的弧的度数为120°,则可知∠CAD=60°,所以只要证AC=AD即可.欲证AC=AD,则要证∠ACD=∠ADC.因这两个角不是圆周角,要转化为圆周角.考虑到B、E是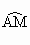 、 、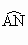 的中点,故应有等角.所以可以连接AB、AE构造等角. 的中点,故应有等角.所以可以连接AB、AE构造等角. |


科目:初中数学 来源: 题型:
 8、如图所示,?ABCD中E是BC的中点,连接AE并延长交DC的延长线于F.
8、如图所示,?ABCD中E是BC的中点,连接AE并延长交DC的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,A、B是双曲线 y=
如图所示,A、B是双曲线 y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com