
【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y= ![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.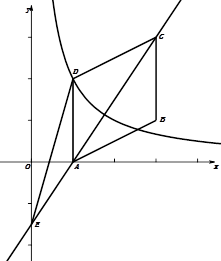
(1)求此双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△ CDE的面积.
【答案】
(1)
解:∵在平行四边形ABCD中,
点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),
∴点D的坐标是(1,2),
∵双曲线y= ![]() (k≠0,x>0)过点D,
(k≠0,x>0)过点D,
∴2= ![]() ,得k=2,
,得k=2,
即双曲线的解析式是:y= ![]() ;
;
(2)
解:∵直线AC交y轴于点E,
∴S△CDE=S△EDA+S△ADC= ![]() ,
,
即△CDE的面积是3.
【解析】(1)根据点A、B、C的坐标以及平行四边形的性质即可得出点D的坐标,再根据反比例函数图象上点的坐标特征即可求出双曲线的解析式;
(2)根据点E在y轴上,可得出点E的横坐标是0,再根据点A、C、D的坐标利用三角形的面积公式 即可得出△CDE的面积.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°. 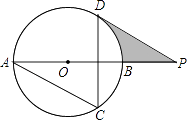
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系. 
(1)小丽驾车的最高速度是km/h;
(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度;
(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2 ![]() .
. 
(1)利用尺规作线段AC的垂直平分线DE,垂足为E,交AB于点D,(保留作图痕迹,不写作法)
(2)若△ADE的周长为a,先化简T=(a+1)2﹣a(a﹣1),再求T的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=40°,BC=3,分别以点B,C为圆心,BC长为半径在BC右侧画弧,两弧交于点D,与AB,AC的延长线分别交于点E,F,则弧DE和弧DF的长度和为( ) 
A.![]()
B.![]()
C.![]()
D.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E,G是 ![]() 的中点,连结AD,AG,CD,则下列结论不一定成立的是( )
的中点,连结AD,AG,CD,则下列结论不一定成立的是( ) 
A.CE=DE
B.∠ADG=∠GAB
C.∠AGD=∠ADC
D.∠GDC=∠BAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林部门决定利用现有的349盆甲种花卉和295盆乙种花卉搭配A、B两种园艺造型共50个,摆放在迎宾大道两侧.已知搭配一个A种造型需甲种花卉8盆,乙种花卉4盆;搭配一个B种造型需甲种花卉5盆,乙种花卉9盆.
(1)某校九年级某班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的成本是200元,搭配一个B种造型的成本是360元,试说明(1)中哪种方案成本最低,最低成本是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com