
 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为3cm2,则△BEF的面积=$\frac{3}{4}$cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为3cm2,则△BEF的面积=$\frac{3}{4}$cm2. 分析 根据三角形的中线把三角形分成两个面积相等的三角形解答.
解答 解:∵点E是AD的中点,
∴S△ABE=$\frac{1}{2}$S△ABD,S△ACE=$\frac{1}{2}$S△ADC,
∴S△ABE+S△ACE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×3=$\frac{3}{2}$,
∴S△BCE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×3=$\frac{3}{2}$,
∵点F是CE的中点,
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×$\frac{3}{2}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$cm2.
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
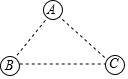 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )
如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个农贸市场,使农贸市场到三个小区的距离均相等,则超市应建在( )| A. | 在三个内角角平分线的交点处 | B. | 在三条高线的交点处 | ||
| C. | 在三条中线的交点处 | D. | 在三条边垂直平分线的交点处 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
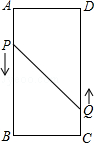 如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3或12 | B. | 12或27 | C. | 40或8 | D. | 3或12或27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
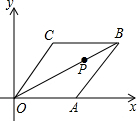 已知菱形OABC在平面直角坐标系中的位置如图所示,顶点A在x轴的正半轴上,OB=4$\sqrt{3}$,∠COA═60°,点P是对角线OB上的一个动点,点D的坐标为(0,1),则CP+DP的最小值为( )
已知菱形OABC在平面直角坐标系中的位置如图所示,顶点A在x轴的正半轴上,OB=4$\sqrt{3}$,∠COA═60°,点P是对角线OB上的一个动点,点D的坐标为(0,1),则CP+DP的最小值为( )| A. | 5 | B. | $\sqrt{17}$ | C. | 4 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com