
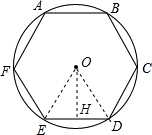
 解:连接OE、OD,
解:连接OE、OD,
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
3
| ||
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
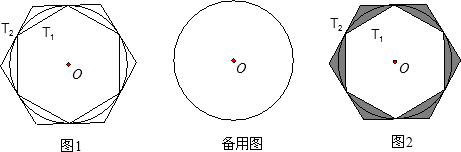
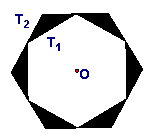
如图一,有一个圆O和两个正六边形T1,T2.T1的六个顶点都在圆周上,T2的六条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)请你在备用图中画出圆O的内接正六边形,并简要写出作法;
(2)设圆O的半径为R,求T1,T2的边长(用含R的式子表示);
(3)设圆O的半径为R,求图二中阴影部分的面积(用含R的式子表示).


图一 备用图 图二
查看答案和解析>>
科目:初中数学 来源:2009-2010学年江西省师大附中九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com