
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹży=©![]() x+bµÄĶ¼Ļó¾¹żµćA£Ø2£¬3£©£¬AB”ĶxÖį£¬“¹×ćĪŖB£¬Į¬½ÓOA£®
x+bµÄĶ¼Ļó¾¹żµćA£Ø2£¬3£©£¬AB”ĶxÖį£¬“¹×ćĪŖB£¬Į¬½ÓOA£®
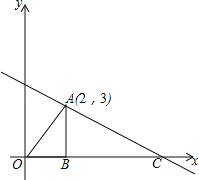
£Ø1£©Ēó“ĖŅ»“ĪŗÆŹżµÄ½āĪöŹ½£¬²¢Ēó³öŅ»“ĪŗÆŹżÓėxÖįµÄ½»µćCµÄ×ų±ź£»
£Ø2£©ÉčµćPĪŖÖ±Ļßy=©![]() x+bŌŚµŚŅ»ĻóĻŽÄŚµÄĶ¼ĻóÉĻµÄŅ»¶Æµć£¬Ēó”÷OBPµÄĆ껿SÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæxµÄ·¶Ī§£»
x+bŌŚµŚŅ»ĻóĻŽÄŚµÄĶ¼ĻóÉĻµÄŅ»¶Æµć£¬Ēó”÷OBPµÄĆ껿SÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæxµÄ·¶Ī§£»
£Ø3£©ÉčµćMĪŖ×ų±źÖįÉĻŅ»µć£¬ĒŅS”÷MAC=24£¬Ö±½ÓŠ“³öĖłÓŠĀś×ćĢõ¼žµÄµćMµÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©Ņ»“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=©![]() £®µćCµÄ×ų±źĪŖ£Ø8£¬0£©£®
£®µćCµÄ×ų±źĪŖ£Ø8£¬0£©£®
£Ø2£©S=©![]() £Ø0£¼x£¼8£©£®
£Ø0£¼x£¼8£©£®
£Ø3£©µćMµÄ×ų±źĪŖM£Ø©8£¬0£©»ņM£Ø24£¬0£©»ņM£Ø0£¬12£©»ņM£Ø0£¬©4£©£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©½«µćAµÄ×ų±ź“śČėŅ»“ĪŗÆŹżµÄ½āĪöŹ½µĆ£ŗ©![]() ”Į2+b=3£¬½āµĆb=4£¬ĒóµĆŅ»“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=©
”Į2+b=3£¬½āµĆb=4£¬ĒóµĆŅ»“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=©![]() +4£¬½«y=0“śČė½āµĆx=8£¬µćCµÄ×ų±źĪŖ£Ø8£¬0£©£»
+4£¬½«y=0“śČė½āµĆx=8£¬µćCµÄ×ų±źĪŖ£Ø8£¬0£©£»
£Ø2£©¹żµćP×÷PD”ĶOC£¬“¹×ćĪŖD£®ÉčµćPµÄ×ų±źĪŖ£Øx£¬©![]() £©£¬ŌņDP=
£©£¬ŌņDP=![]() £¬ÓɵćAµÄ×ų±źĪŖ£Ø2£¬3£©æÉÖŖµćBµÄ×ų±źĪŖ£Ø2£¬0£©£¬¹Ź“ĖOB=2£¬ÓÉČż½ĒŠĪµÄĆ껿¹«Ź½æÉÖŖS=
£¬ÓɵćAµÄ×ų±źĪŖ£Ø2£¬3£©æÉÖŖµćBµÄ×ų±źĪŖ£Ø2£¬0£©£¬¹Ź“ĖOB=2£¬ÓÉČż½ĒŠĪµÄĆ껿¹«Ź½æÉÖŖS=![]() £»
£»
£Ø3£©·ÖĪŖµćMŌŚxÖįÉĻŗĶyÖįÉĻĮ½ÖÖĒéæö»³öĶ¼ŠĪ£¬Č»ŗóŌŁøł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½ĮŠ³ö¹ŲÓŚµćM×ų±źµÄ·½³ĢĒó½ā¼“æÉ£®
½ā£ŗ£Ø1£©”ß½«x=2£¬y=3“śČėµĆ£ŗ©![]() ”Į2+b=3£¬½āµĆ£ŗb=4£¬
”Į2+b=3£¬½āµĆ£ŗb=4£¬
”ąŅ»“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=©![]() £®
£®
”ß½«y=0“śČėµĆ£ŗ![]() =0£¬½āµĆx=8£®
=0£¬½āµĆx=8£®
”ąµćCµÄ×ų±źĪŖ£Ø8£¬0£©£®
£Ø2£©ČēĶ¼1ĖłŹ¾£ŗ¹żµćP×÷PD”ĶOC£¬“¹×ćĪŖD£®
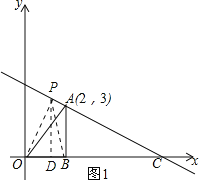
ÉčµćPµÄ×ų±źĪŖ£Øx£¬©![]() £©£¬ŌņDP=
£©£¬ŌņDP=![]() £®
£®
”ßAB”ĶOC£¬A£Ø2£¬3£©£¬
”ąµćB£Ø2£¬0£©£®
”ąOB=2£®
”ą![]() =
=![]() =©
=©![]() £®
£®
”ąS=©![]() £Ø0£¼x£¼8£©£®
£Ø0£¼x£¼8£©£®
£Ø3£©ČēĶ¼2ĖłŹ¾£ŗ

¢Łµ±µćMŌŚxÖįÉĻĒŅĪ»ÓŚµćC×ó²ąŹ±£¬ÉčµćMµÄ×ų±źĪŖ£Øa£¬0£©£¬ŌņMC=8©a£®
”ßS”÷MAC=24£¬
”ą![]() £¬¼“
£¬¼“![]() £®
£®
½āµĆ£ŗa=©8£®
”ąµćMµÄ×ų±źĪŖ£Ø©8£¬0£©£®
¢Śµ±µćMĪ»ÓŚµćM”䓦Ź±£¬ÉčµćM”äµÄ×ų±źĪŖ£Øa£¬0£©£¬ŌņM”äC=a©8£®
”ßS”÷MAC=24£¬
”ą![]() £¬¼“
£¬¼“![]() £®
£®
½āµĆ£ŗa=24£®
”ąµćMµÄ×ų±źĪŖ£Ø24£¬0£©£®
ČēĶ¼3ĖłŹ¾£ŗ
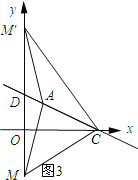
”ß½«x=0“śČėy=©![]() µĆ£ŗy=4£®
µĆ£ŗy=4£®
”ąµćDµÄ×ų±źĪŖ£Ø0£¬4£©£®
¢Ūµ±µćMĪ»ÓŚµćDµÄĻĀ·½Ź±£¬ÉčµćMµÄ×ų±źĪŖ£Ø0£¬a£©£¬ŌņDM=4©a£®
”ßS”÷ACM=SMCD©S”÷MDA=24£¬
”ą![]() ©
©![]() =24£®
=24£®
½āµĆ£ŗa=©4£®
”ąµćMµÄ×ų±źĪŖ£Ø0£¬©4£©£®
¢Üµ±µćMĪ»ÓŚµćM”䓦Ź±£¬ÉčµćMµÄ×ų±źĪŖ£Ø0£¬a£©£¬ŌņDM=a©4£®
”ßS”÷ACM=SMCD©S”÷MDA=24£¬
”ą![]() =24£®
=24£®
½āµĆ£ŗa=12£®
”ąµćMµÄ×ų±źĪŖ£Ø0£¬12£©£®
×ŪÉĻĖłŹö£¬µćMµÄ×ų±źĪŖM£Ø©8£¬0£©»ņM£Ø24£¬0£©»ņM£Ø0£¬12£©»ņM£Ø0£¬©4£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¼×ŹĒŅ»øö³¤ĪŖ2m£¬æķĪŖ2nµÄ³¤·½ŠĪ£¬ŃŲĶ¼ÖŠµÄŠéĻß¼ō³ÉĖÄøöČ«µČµÄŠ”³¤·½ŠĪ£¬ŌŁ°“Ķ¼ŅŅĪ§³ÉŅ»øö½Ļ“óµÄÕż·½ŠĪ£®

£Ø1£©ĒėÓĆĮ½ÖÖ·½·Ø±ķŹ¾Ķ¼ÖŠŅõÓ°²æ·ÖĆ껿£ØÖ»Šč±ķŹ¾£¬²»±Ų»Æ¼ņ£©£»
£Ø2£©±Č½Ļ£Ø1£©Į½ÖÖ½į¹ū£¬ÄćÄܵƵ½ŌõŃłµÄµČĮæ¹ŲĻµ£æ
ĒėÄćÓĆ£Ø2£©ÖŠµĆµ½µČĮæ¹ŲĻµ½ā¾öĻĀĆęĪŹĢā£ŗČē¹ūm©n=5£¬mn=14£¬Ēóm+nµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ±ß³¤ĪŖ1øöµ„Ī»³¤¶ČµÄŠ”Õż·½ŠĪ×é³ÉµÄĶųøńÖŠ£¬øų³öĮĖøńµć”÷ABC£Ø¶„µćŹĒĶųøńĻߵĽ»µć£©£®

£Ø1£©ĻČ½«”÷ABCŹśÖ±ĻņÉĻĘ½ŅĘ6øöµ„Ī»£¬ŌŁĖ®Ę½ĻņÓŅĘ½ŅĘ1øöµ„Ī»µĆµ½”÷A1B1C1£¬Ēė»³ö”÷A1B1C1£»
£Ø2£©½«”÷A1B1C1ČĘB1µćĖ³Ź±ÕėŠż×Ŗ90”ć£¬µĆ”÷A2B1C2£¬Ēė»³ö”÷A2B1C2£»
£Ø3£©Ēó£Ø2£©ÖŠµćA1Šż×Ŗµ½µćA2Ėł¾¹żµÄ»”³¤![]() £Ø½į¹ū±£Įō¦Š£©£®
£Ø½į¹ū±£Įō¦Š£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¼Ę»®æŖÉč4ĆÅŃ”ŠŽæĪ£ŗŅōĄÖ”¢»ę»”¢ĢåÓż”¢Īčµø£¬Ń§Š£²ÉČ”Ė껜³éŃłµÄ·½·Ø½ųŠŠĪŹ¾ķµ÷²é£ØĆæøö±»µ÷²éµÄѧɜ±ŲŠėŃ”Ōń¶ųĒŅÖ»ÄÜŃ”ŌńĘäÖŠŅ»ĆÅ£©£¬¶Ōµ÷²é½į¹ū½ųŠŠĶ³¼Ęŗ󣬻ęÖĘĮĖČēĻĀ²»ĶźÕūµÄĮ½øöĶ³¼ĘĶ¼£®
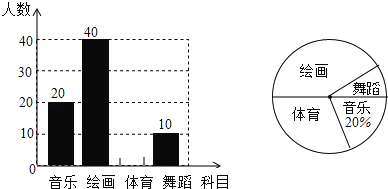
øł¾ŻŅŌÉĻĶ³¼ĘĶ¼Ģį¹©µÄŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©“Ė“Īµ÷²é³éČ”µÄѧɜČĖŹżĪŖa= ČĖ£¬ĘäÖŠŃ”Ōń”°»ę»”±µÄѧɜČĖŹżÕ¼³éŃłČĖŹżµÄ°Ł·Ö±ČĪŖb= £»
£Ø2£©²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©ČōøĆŠ£ÓŠ2000Ćūѧɜ£¬Ēė¹Ą¼ĘČ«Š£Ń”Ōń”°»ę»”±µÄѧɜ“óŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
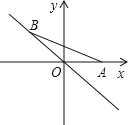
”¾ĢāÄæ”æČēĶ¼£¬µćAµÄ×ų±źĪŖ£Ø1£¬0£©£¬µćBŌŚÖ±Ļßy=©xÉĻŌĖ¶Æ£¬µ±Ļ߶ĪAB×ī¶ĢŹ±£¬µćBµÄ×ų±źĪŖ£Ø £©
A£®£Ø0£¬0£© B£®£Ø![]() £¬©
£¬©![]() £© C£®£Ø
£© C£®£Ø![]() £¬©
£¬©![]() £© D£®£Ø©
£© D£®£Ø©![]() £¬
£¬![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬AB=AC£¬AD”ĶBC£¬CE”ĶAB£¬AE=CE£®ĒóÖ¤£ŗ
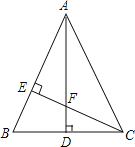
£Ø1£©”÷AEF”Õ”÷CEB£»
£Ø2£©AF=2CD£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬µćCŌŚ”ŃOÉĻ£¬”ĻCABµÄĘ½·ÖĻß½»”ŃOÓŚµćD£¬¹żµćD×÷ACµÄ“¹Ļß½»ACµÄŃÓ³¤ĻßÓŚµćE£¬Į¬½ÓBC½»ADÓŚµćF£®
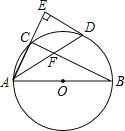
£Ø1£©²ĀĻėEDÓė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ²ĀĻė£»
£Ø2£©ČōAB=6£¬AD=5£¬ĒóAFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
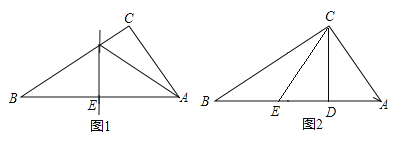
”¾ĢāÄæ”æŌŚŹżŃ§ŹµŃéæĪÉĻ£¬Ąī¾²Ķ¬Ń§¼ōĮĖĮ½ÕÅÖ±½ĒČż½ĒŠĪÖ½Ę¬£¬½ųŠŠČēĻĀµÄ²Ł×÷£ŗ
²Ł×÷Ņ»£ŗČēĶ¼1£¬½«Rt”÷ABCÖ½Ę¬ŃŲijĢõÖ±ĻßÕŪµž£¬Ź¹Š±±ßĮ½øö¶ĖµćAÓėBÖŲŗĻ£¬ÕŪŗŪĪŖDE£®
£Ø1£©Čē¹ūAC£½5cm£¬BC£½7cm£¬æɵƔ÷ACDµÄÖܳ¤ĪŖ £»
£Ø2£©Čē¹ū”ĻCAD£ŗ”ĻBAD=1£ŗ2£¬æɵƔĻBµÄ¶ČŹżĪŖ £»
²Ł×÷¶ž£ŗČēĶ¼2£¬Ąī¾²ÄĆ³öĮķŅ»ÕÅRt”÷ABCÖ½Ę¬£¬½«Ö±½Ē±ßACŃŲÖ±ĻßCDÕŪµž£¬Ź¹µćAÓėµćEÖŲŗĻ£¬ČōAB£½10cm£¬BC£½8cm£¬ĒėĒó³öBEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŗÆŹży=![]() ŗĶy=
ŗĶy=![]() µÄĶ¼Ļó·Ö±šŹĒl1ŗĶl2£¬ÉčµćPŌŚl1ÉĻ£¬PC”ĶxÖį£¬“¹×ćĪŖC£¬½»l2ÓŚµćA£¬PD”ĶyÖį£¬“¹×ćĪŖD£¬½»l2ÓŚµćB£¬ŌņČż½ĒŠĪPABµÄĆ껿ĪŖ£Ø £©
µÄĶ¼Ļó·Ö±šŹĒl1ŗĶl2£¬ÉčµćPŌŚl1ÉĻ£¬PC”ĶxÖį£¬“¹×ćĪŖC£¬½»l2ÓŚµćA£¬PD”ĶyÖį£¬“¹×ćĪŖD£¬½»l2ÓŚµćB£¬ŌņČż½ĒŠĪPABµÄĆ껿ĪŖ£Ø £©

A£®8 B£®9 C£®10 D£®11
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com