
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.

【答案】(1)y=-x+6;(2)M(0,![]() );(3)(0,-2)或(0,-6).
);(3)(0,-2)或(0,-6).
【解析】
(1)设AB的函数解析式为:y=kx+b,把A、B两点的坐标代入解方程组即可.
(2)作点B关于y轴的对称点B′,则B′点的坐标为(-6,0),连接AB′则AB′为MA+MB的最小值,根据A、B′两点坐标可知直线AB′的解析式,即可求出M点坐标,(3)分别考虑∠MAB为直角时直线MA的解析式,∠ABM′为直角时直线BM′的解析式,求出M点坐标即可,
(1)设直线AB的函数解析式为y=kx+b,则![]() 解方程组得
解方程组得![]()
直线AB的函数解析式为y= -x+6,
(2)如图作点B关于y轴的对称点B′,则点B′的坐标为(-6,0),连接AB′则AB′为MA+MB的最小值,设直线AB′的解析式为y=mx+n,则![]() ,
,
解方程组得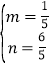
所以直线AB′的解析式为![]() ,
,
当x=0时,y=![]() ,
,
所以M点的坐标为(0,![]() ),
),
(3)有符合条件的点M,理由如下:
如图:因为△ABM是以AB为直角边的直角三角形,
当∠MAB=90°时,直线MA垂直直线AB,
∵直线AB的解析式为y=-x+6,
∴设MA的解析式为y=x+b,
∵点A(4,2),
∴2=4+b,
∴b=-2,
当∠ABM′=90°时,BM′垂直AB,
设BM′的解析式为y=x+n,
∵点B(6,0)
∴6+n=0
∴n=-6,
即有满足条件的点M为(0,-2)或(0,-6).


科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城科技公司生产销售一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分,经核算,2014年该产品各部分成本所占比例约为2:a:1.且2014年该产品的技术成本、制造成本分别为400万元、1400万元.
(1)确定a的值,并求2014年产品总成本为多少万元;
(2)为降低总成本,该公司2015年及2016年增加了技术成本投入,确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%),制造成本在这两年里都比前一年减少一个相同的百分数2m;同时为了扩大销售量,2016年的销售成本将在2014年的基础上提高10%,经过以上变革,预计2016年该产品总成本达到2014年该产品总成本的 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
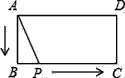
【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
A. 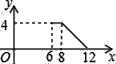 B.
B. 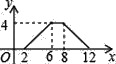 C.
C. 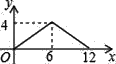 D.
D. 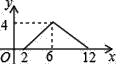
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知直线l1经过原点O 及A(2,2 ![]() )两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B.
)两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B. 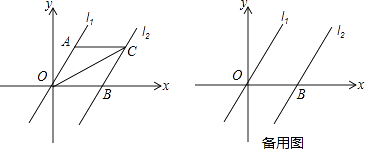
(1)求直线l2的函数表达式;
(2)作∠AOB 的平分线交直线l2于点C,连接AC.求证:四边形OACB是菱形;
(3)设点P 是直线l2上一点,以P 为圆心,PB 为半径作⊙P,当⊙P 与直线l1相切时,请求出圆心P 点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,它的图象与
,它的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 点
点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________;
的坐标为________;
![]() 画出此函数图象;
画出此函数图象;
![]() 画出该函数图象向下平移
画出该函数图象向下平移![]() 个单位长度后得到的图象;
个单位长度后得到的图象;
![]() 写出一次函数
写出一次函数![]() 图象向下平移
图象向下平移![]() 个单位长度后所得图象对应的表达式.
个单位长度后所得图象对应的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=10cm,BC=8cm、点P从A出发,沿A、B、C、D路线运动,到D停止;点P的速度为每秒1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,△APD的面积S1(cm2)与x(秒)的函数关系图象;
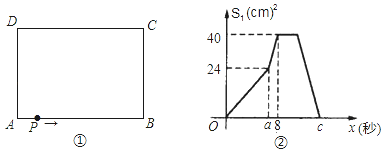
(1)根据图②中提供的信息,求a、b及图②中c的值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的函数关系式;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com